Vectorization in Haskell

Abhiroop Sarkar

@catamorphic

Superword Level Parallelism in the Glasgow Haskell Compiler

A CUSTOMARY RITUAL

Moore's Law is over :(

Types of Parallel Machines

Flynn

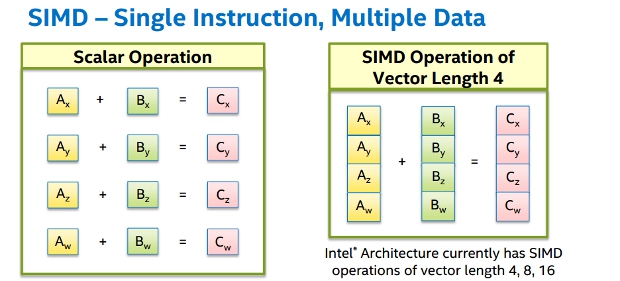
Single Instruction Multiple Data

Simd

Cray 1 - the first supercomputer to implement the vector processor design

x86 Instruction Set

  • Intel
    • SSE (Intel P6, 1999)
    • SSE2 (Intel Pentium M, 2003)
    • SSE3 (NetBurst - Pentium 4, 2004)
    • SSE4.1 (Intel Core, 2006)
    • SSE4.2 (Nehalem, 2008)
    • AVX (SandyBridge, 2011)
    • AVX2 (Haswell, 2013)
    • AVX512 (Canon Lake, 2018)
  • AMD

Compiler Support

  • GCC
  • LLVM Toolchain
  • Dyalog APL

Can a purely functional language support vectorisation?

The question is incomplete...

Can a purely functional language support vectorisation, preserving its original syntax and semantics while being as efficient as low level systems programming languages?

Parsing the previous statement :

  • High Performance
  • Declarative Syntax

We answer that in 2 steps.

  • a low level code generator
  • a high level vector programming library

Original Idea

LLVM backend for NESL

NESL : An ML Dialect by Guy Blelloch (CMU) which supports Nested Data Parallelism

Disadvantages

  • Compiler written in Common Lisp
  • Flattens almost every level of parallelism
  • Small prototype language without a great I/O manager
  • Hard to debug

Enter Haskell

Glasgow Haskell Compiler (GHC)

State of the art optimising compiler

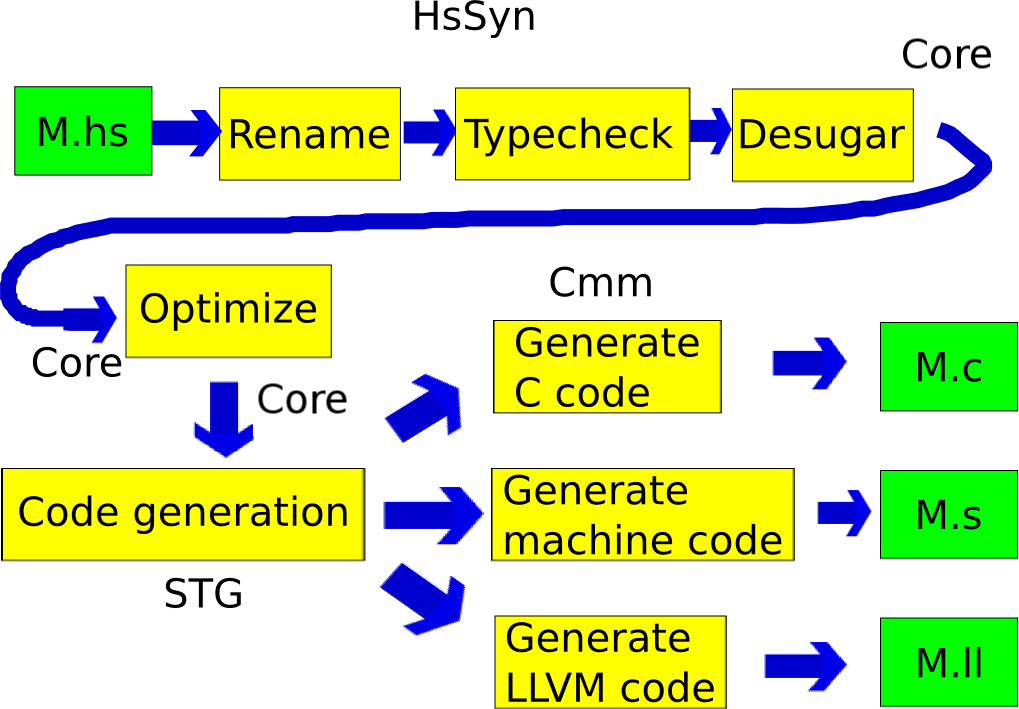
ghcpipe

Where have we made code changes?

  • Parser
  • Add some new runtime representations
  • STG -> Cmm bridge
  • Cmm (multiple layers)
  • Native code generator (x86 Assembly)

Fundamental Code changes:

compiler/nativeGen/Format.hs

data Format = ...
            | VecFormat !Length !ScalarFormat !Width

type Length = Int

data Width = ... | W128 | W256 | W512

compiler/nativeGen/x86/Instr.hs

data Instr = VBROADCAST Format AddrMode Reg
           | VEXTRACT   Format Operand Reg Operand
           ...
           -- number of other instructions like vector move, 
           -- shuffle, arithmetic, logical x86 instructions

compiler/cmm/CmmMachOp.hs

data MachOp = MO_VF_Broadcast Length Width
            | MO_VF_Insert ....

70% code changes in compiler/nativeGen/X86/CodeGen.hs

Lots of seg-faults and code reviews later

EXAMPLE : BROADCAST

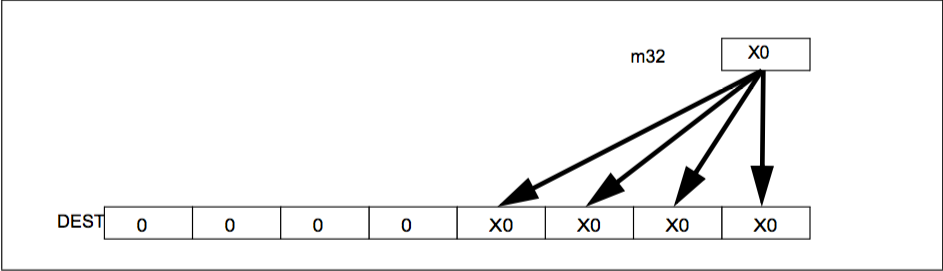
broadcast

phases

  • low level code generator changes
    • Float and Double SIMD support
    • redefine integers to support SIMD

The user-level API

 -- constructors
packFloatX4#      :: (# Float#, Float#, Float#, Float# #) -> FloatX4#
broadcastFloatX4# :: Float# -> FloatX4#
 -- destructors
unpackFloatX4# :: FloatX4# (# Float#, Float#, Float#, Float# #)
 -- operations
plusFloatX4#   :: FloatX4# -> FloatX4# -> FloatX4#
minusFloatX4#  :: FloatX4# -> FloatX4# -> FloatX4#
timesFloatX4#  :: FloatX4# -> FloatX4# -> FloatX4#
divideFloatX4# :: FloatX4# -> FloatX4# -> FloatX4#

SSE as well as AVX support

Previously we had

data Int8  = I8#  Int#
data Int16 = I16# Int#
data Int32 = I32# Int#
data Int64 = I64# Int#

Now GHC has :

Int8#, Word8#, Int16#, Word16#, Int32#, Word32#, Int64#, Word64#

Example : Vectorizing dot product

This spoils the declarative nature of Haskell!

Imperative languages have powerful vector programming libraries

Lift-Vector

Polymorphic SIMD functions for vector programming

Lift-vector provides two interfaces

  • Data.Primitive
  • Data.Operations

Data.Primitive

class (Num v, Real (Elem v)) => SIMDVector v where
    type Elem v

    type ElemTuple v

    nullVector       :: v
    vectorSize       :: v -> Int
    elementSize      :: v -> Int
    broadcastVector  :: Elem v -> v
    mapVector        :: (Elem v -> Elem v) -> v -> v
    zipVector        :: (Elem v -> Elem v -> Elem v) -> v -> v -> v
    foldVector       :: (Elem v -> Elem v -> Elem v) -> v -> Elem v
    sumVector        :: v -> Elem v
    packVector       :: ElemTuple v -> v
    unpackVector     :: v -> ElemTuple v

From github/ajscholl/primitive

What does dot product look like with this?

Data.Operations

class (Num a, Num b) =>
      ArithVector t a b
  where
  -- | The folding function should be commutative.
  fold :: (a -> a -> a) -> (b -> b -> b) -> b -> t b -> b
  zipVec ::
       (a -> a -> a) -> (b -> b -> b) -> t b -> t b -> t b
  fmap  :: (a -> a) -> (b -> b) -> t b -> t b
  -- | Work efficient Blelloch Scan
  scanb :: (a -> a -> a) -> (b -> b -> b) -> b -> t b -> t b

Vectorised Containers

  • Vector Lists
  • Vector Arrays (Shape polymorphic)

Vector Lists

newtype VecList a = VecList [a]

A wrapper over plain lists

Vector Arrays

Wrappers around unboxed vectors.

unboxed


import qualified Data.Vector.Unboxed as U

data VecArray sh a = VecArray !sh (U.Vector a)

Shape Polymorphism

Inspired from Repa, Accelerate, Ypnos and other array libraries
data Z = Z
data tail :. head = !tail :. !head

type DIM0 = Z
type DIM1 = DIM0 :. Int
type DIM2 = DIM1 :. Int
type DIM3 = DIM2 :. Int

class Eq sh => Shape sh where
   toIndex :: sh -> sh -> Int
   ...

instance Shape Z where
   toIndex _ _ = 0

instance Shape sh => Shape (sh :. Int) where
   toIndex (sh1 :. sh2) (sh1' :. sh2')
               = toIndex sh1 sh1' * sh2 + sh2'

What does dot product look like with the parallel operators?

How are the Data.Operations operators implemented?

ZIP

zip

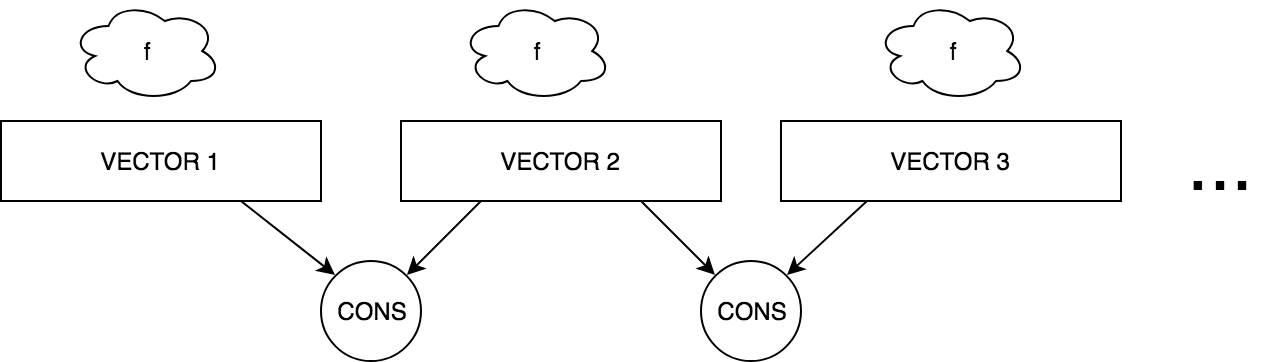
MAP

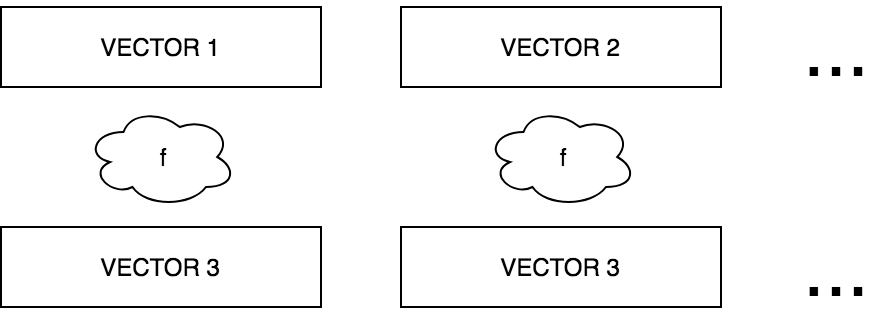
map

FOLD

fold

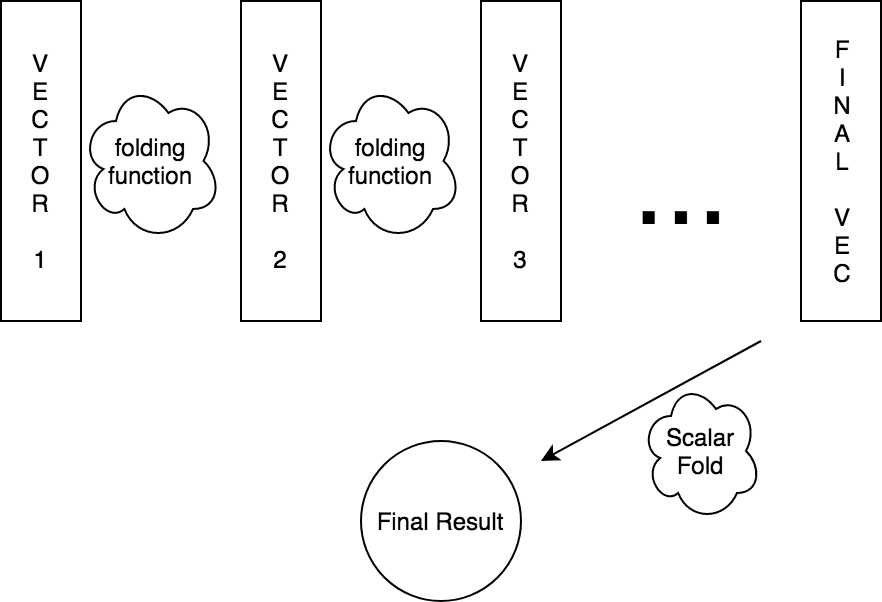
SCAN

scan or prefix sum looks like an inherently sequential operation

> scanl (+) 0 [1, 2, 3, 4, 5, 6, 7, 8]
> [0,1,3,6,10,15,21,28,36]

HILLIS AND STEELE SCAN

fold

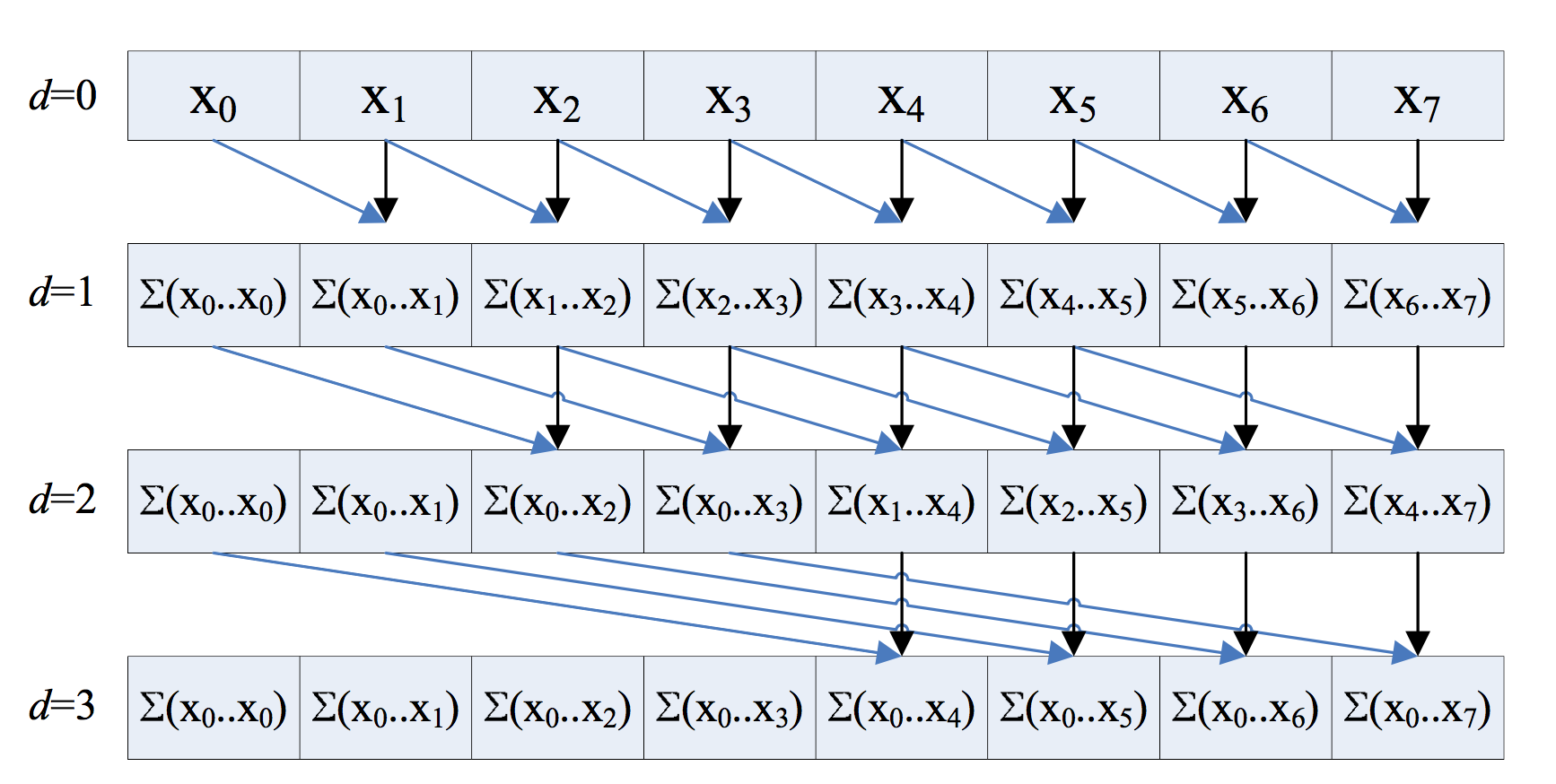
This is parallel but does O(n log2 n) work.

Sequential scan does O(n) operations.

Analysis of parallel algorithms

How long it would take if it were fully sequential (work)

How long it would take if it were as parallel as possible (span)

"Programming parallel algorithms" - Guy Blelloch, 1996

Can we have a work efficient parallel scan?

BLELLOCH SCAN

UPSWEEP

upsweep

DOWNSWEEP

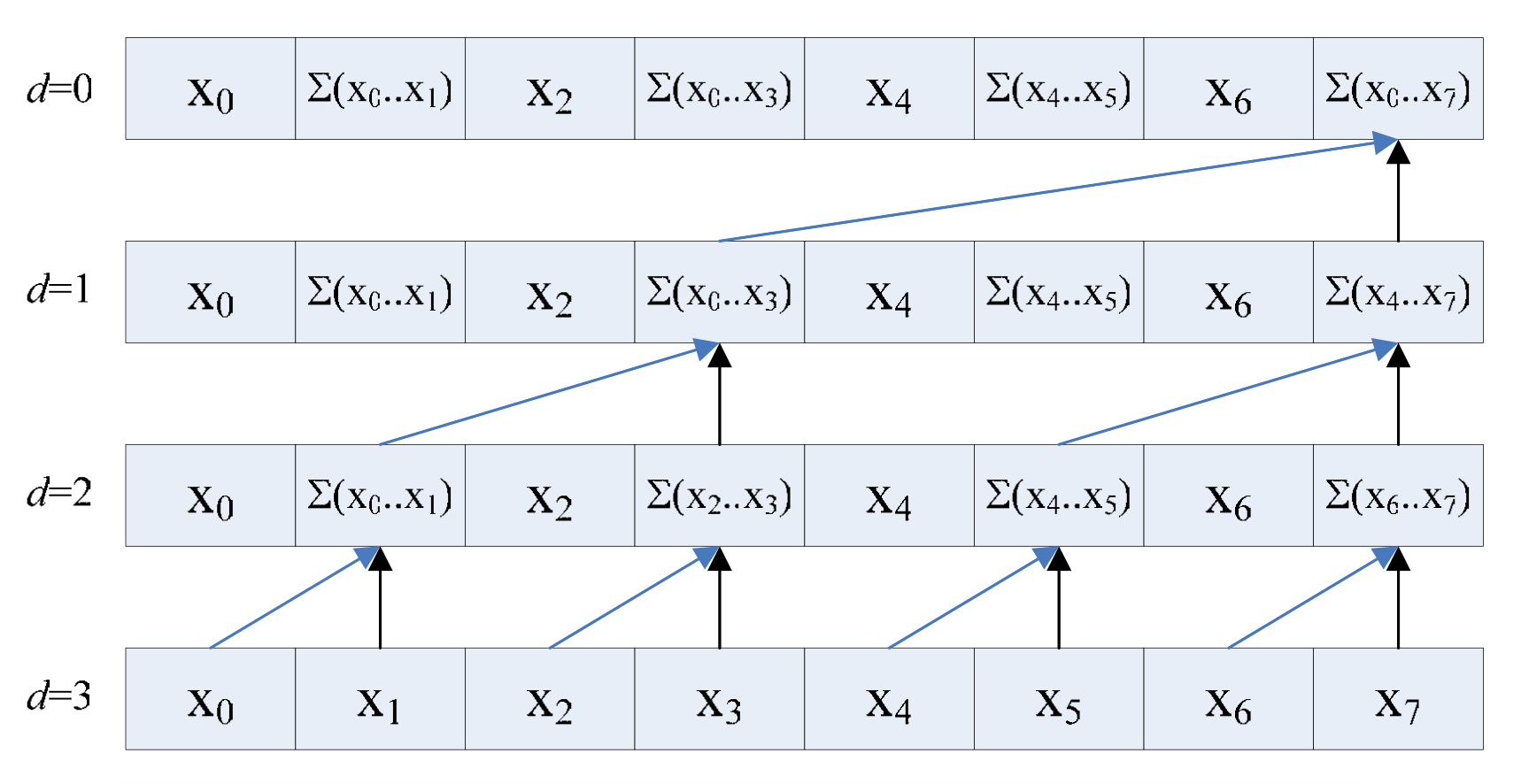
downsweep

So are scans really that useful?

APPLICATIONS OF PARALLEL SCAN

  • Lexical string comparison
  • Adding multi precison numbers
  • Polynomial evaluation
  • Radix Sort
  • Implement parallel quicksort
  • ...

"Prefix sums and their applications." - Guy Blelloch, 1990

Q: So are folds, maps , zips and scans sufficient enough combinators?

A: Maybe

Examples

Good benchmarks

Heavy reads and less write

Pearson Correlation Coefficient

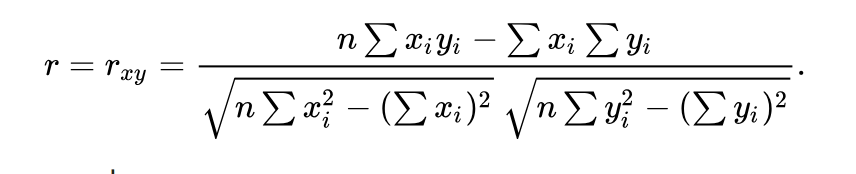
coeff

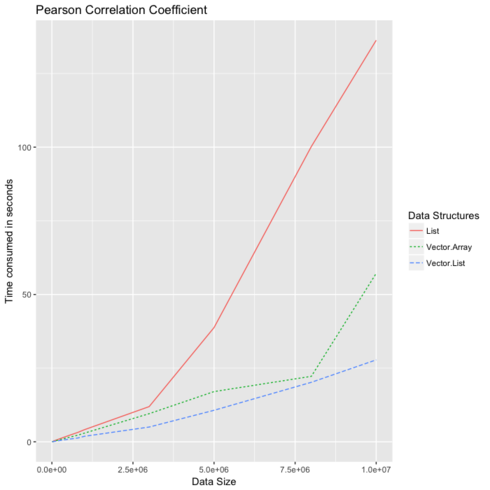
pearson

Bad benchmarks

Heavy writes

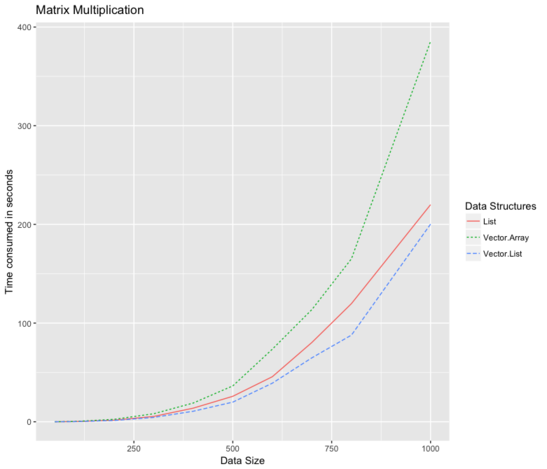
mmult

Writes perform better now via thawing and freezing inside the ST monad.

Future Work

  • Automatic Vectorisation
    • Loop vectorisation
    • Throttled SLP algorithm
  • An ideal cost model for vectorisation
  • Mutable arrays supporting in place writes (inspiration from Futhark)
  • More vectorised data structures
  • Improving the API of lift-vector
  • Alternate IR like SSA inside GHC

Almost any paper by Guy Blelloch

blelloch

From the Haskell side:

"Automatic SIMD vectorization for Haskell" - Petersen, Orchard, Glew

"Exploiting vector instructions with generalized stream fusion" - Mainland, Leschinskiy, Jones

If you are lazy read my 5k words summary:

https://abhiroop.github.io/vectorization.pdf

Conclusion

Haskell is already a great parallel language!

Haskell could be the state of art in vector programming!

Special Thanks to

  • Carter Tazio Schonwald (my GSoC mentor)
  • Graham Hutton (my thesis supervisor)
  • Ben Gamari (my second GSoC mentor)
  • Google for funding Haskell.org as part of GSoC 2018

Looking for PhD Advisors in the field of

High performance functional programming

(^ Not an oxymoron!)

THANK YOU FOR LISTENING

Contact me if this interests you:

Email : asiamgenius@gmail.com

Twitter : @catamorphic

Abhiroop Sarkar

https://github.com/Abhiroop/lift-vector