While Haskell is steadily gaining mainstream adoption in the industry, it still remains one of the most viable languages used as a teaching medium. Even if we strip the fancy type level features in Haskell, algebraic data types and pattern matching are quite expressive enough to represent a lot of ideas.

In this post I will be looking at the construction and operations of Red Black trees. Of special interest here would be the deletion of nodes, as the operation of delete is inherently opposed to Haskell’s fundamentals of immutability. We will look at these various operations as creating a new version of the tree rather than mutating an existing version, which gives the persistent quality to our data structure.

This post doesn’t use any fancy type level features of Haskell(except at the very end) and assumes only basic familiarity with the language. However the deletion operation is quite involved and requires the reader to be fairly meticulous so as to not miss any of the possible cases.

A red black tree is a type of a binary search tree with the ability to self balance itself. This property of self balancing is highly desirable as a plain binary search tree reduces to O(n) worst case time complexity for search, insert and delete operations. The balancing nature of red black tree gives it a worst case time complexity of O(log n). It is not truly balanced, in the sense that the heights of the various subtrees can differ, but the height of the longest subtree would be a maximum of 2log(n+1), which effectively gives it a balanced nature.

From a practical perspective, it is not expected of you to code out a fully functional red black tree every other day, but it is helpful to know the implementations and understand the trade-offs made so that performance analysis on some critical code can be made.

Notably, TreeMap from the Java collections library is implemented using a Red Black Tree(however it is not a persistent implementation). In practice, most implementations of maps, sets and other useful structures are implemented using balanced binary search trees. Hence without any further ado lets jump into the datatypes.

Defining the tree

We will start by defining 2 colors red and black and use that as a metadata in our actual tree type.

data Color = R | B deriving Show

data Tree a = E | T Color (Tree a) a (Tree a) deriving Show

Now for a red black tree to be balanced it needs to follow a set of invariants. These invariants technically can be encoded into the Haskell type system but to keep the implementation simpler we define it using functions and verify them at runtime. The invariants are:

1. No red node has a red parent or a red node has only black children.
2. Every path from the root node to an empty node contains the same number of black nodes.
3. The root and leaves of the tree are black.

Take some time to internalize these invariants, as they should not be broken under any circumstances. Throughout the rest of the article, these invariants are referred to a number of times by just referring to their serial number. We can relax some of them locally in certain cases but we make sure some other functions at the global level handles the violation and rectifies it. We are going to start by implementing the member function, which basically tells us if the element belongs to the tree or not. This is not very different from a regular BST.

member :: (Ord a) => a -> Tree a -> Bool
member x E    = False
member x (T _ a y b)
  | x < y     = member x a
  | x == y    = True
  | otherwise = member x b

This should be self explanatory. If we find the element we report True otherwise we recurse down the left or right subtree.

Insertion

Now lets look at one of the more involved operations: insert.

The insertion operation was described by Chris Okasaki in his classic book “Purely Functional Data Structures”. The insertion of a node is colored red in the beginning so as not to affect the height. However this might end up violating the first invariant. To restore the first invariant we have to balance the tree recursively. The function looks something like this:

insert :: (Ord a) => a -> Tree a -> Tree a
insert x s = makeBlack $ ins s
  where ins E  = T R E x E
        ins (T color a y b)
          | x < y  = balance color (ins a) y b
          | x == y = T color a y b
          | x > y  = balance color a y (ins b)
        makeBlack (T _ a y b) = T B a y b

The points to notice here in this definition are the functions makeBlack and balance. Minus those functions the insertion is exactly similar to an insert in a BST. The makeBlack function is also a fairly simple function, given a Node it changes the color of the node to black irrespective of the node’s color. The purpose of this function is that, after applying balance recursively the final tree might have 2 consecutive red nodes at the top of the tree. This would be a violation of invariant 1. By blackening the root we restore invariant 1 as well as we invariant 2 stays intact, as only the root of the tree gets colored. A more apt name for the function, perhaps should have been blackenRoot. However this is quite simple.

The trick is now writing and understanding the balance function. Now we know that the insertion might have violated invariant 1 and as a result of which it might have created a tree with 2 consecutive red nodes. So all we have to think is, given the original balanced tree with no violations, what are the possible ways in which a red node might have been inserted which breaks the invariant 1. Let us see: (Due to lack of a red pen I am using a blue pen to represent red nodes. So this is technically a blue black tree. But you get the point):

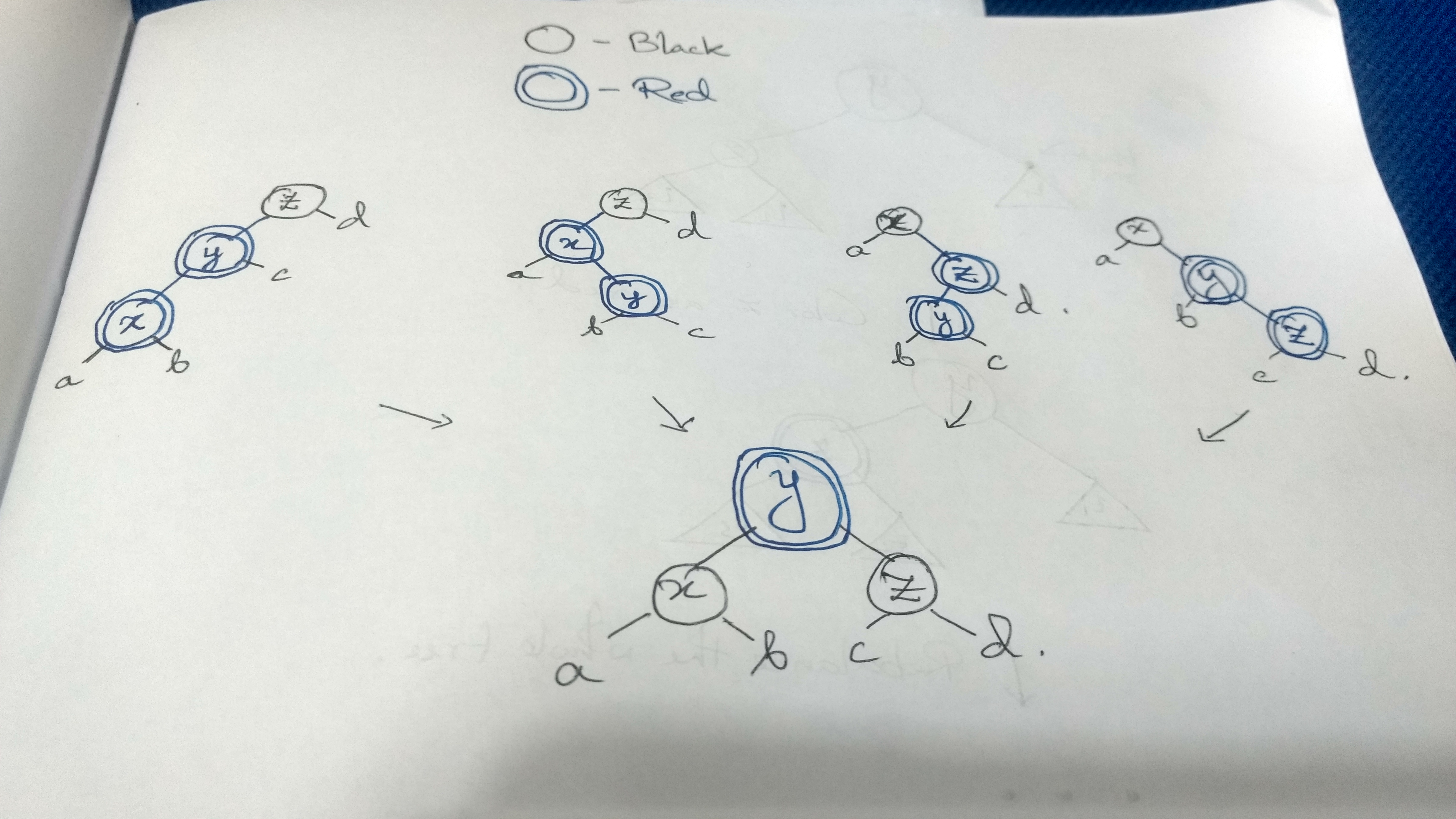
Now algebraic data types and pattern matching makes it very easy to express each case. So if we write out the tree structure as demonstrated in the figure, the 4 cases would look like this:

T B (T R (T R a x b) y c) z d  
T B (T R a x (T R b y c)) z d  
T B a x (T R (T R b y c) z d)  
T B a x (T R b y (T R c z d)) 

So all we have to do is find a way to balance each of the cases. As it is given in the figure, the solution to balancing each of the 4 cases is the exact same. By using this transformation, the tree restores the invariant 1. And invariant 2 stays intact too(Invariant 3 is almost always intact and easiest to enforce). So what happens for the other configurations of the tree? We return the nodes intact. So writing the same in Haskell:

balance :: Color -> Tree a -> a -> Tree a -> Tree a
balance B (T R (T R a x b) y c) z d = T R (T B a x b) y (T B c z d)
balance B (T R a x (T R b y c)) z d = T R (T B a x b) y (T B c z d)
balance B a x (T R (T R b y c) z d) = T R (T B a x b) y (T B c z d)
balance B a x (T R b y (T R c z d)) = T R (T B a x b) y (T B c z d)
balance color a x b = T color a x b

Languages like OCaml and SML support something called OR patterns which make it even simpler to write the function definition where multiple patterns have the same answer. And in fact there is a GHC proposal in progress about adding OR patterns to Haskell. This implementation is much more readable, expressive and most importantly intuitive compared to any other imperative language implementations of the same idea. Writing a red black tree balancing algorithm is a big deal in such languages but with ADTs and pattern matching it literally begs to follow the diagram given above.

Deletion

Now moving on to the delete operation. This one is lot more involved and we will do it step by step.

First a deletion followed by any kind of balancing has the possibility of bubbling a red node to the top, so we need the makeBlack function that we used in the insert function, followed by that we can call an auxiliary del function which will effectively delete the node and balance the tree. In Haskell:

delete :: (Ord a) => a -> Tree a -> Tree a
delete x t = makeBlack $ del x t
  where makeBlack (T _ a y b) = T B a y b

This is fairly simple. Let us explore the del function in depth.

So, in case of the insert function, the balancing of the trees, conveniently unified into a single transformation but that is not the case for delete. The cases of balancing are different but symmetric to each other for the left and right subtrees and we have to handle the 2 cases separately. So we will declare 2 separate function delL and delR for the left and right subtree respectively. And what about the case when we actually arrive at the node which we want to delete? In that case we remove that node and fuse the left and right subtree together. We will look at the fuse function in detail at a later part of this article. So writing the del function:

del :: (Ord a) => a -> Tree a -> Tree a
del x t@(T _ l y r)
  | x < y = delL x t
  | x > y = delR x t
  | otherwise = fuse l r

which literally translates from what we described in the earlier paragraph. So now before delving into the delL and delR function let us try to think about the balancing first. So for the corresponding delL and delR function we will have a balL and balR function which balance the left and right subtrees respectively, when one is shorter than the other. The signature of balL and balR should be dead simple. Given an unbalanced tree it recolors and balances the trees and outputs a balanced tree.

balL :: Tree a -> Tree a

balR :: Tree a -> Tree a

Now as red nodes don’t contribute to the height of the tree and given invariant 1, that red nodes can only have black child, when a deletion of a node occurs, the violation of invariant 2 can happen and the left and right subtree might not be of equal height(Remember only black nodes contribute to the height of the tree.)

balL concerns the cases where deletion has occurred from the left subtree. Hence in balL we can assume that the left subtree is shorter than the right subtree. What are the possible cases?

Case 1: Root node is black and left subtree root is red

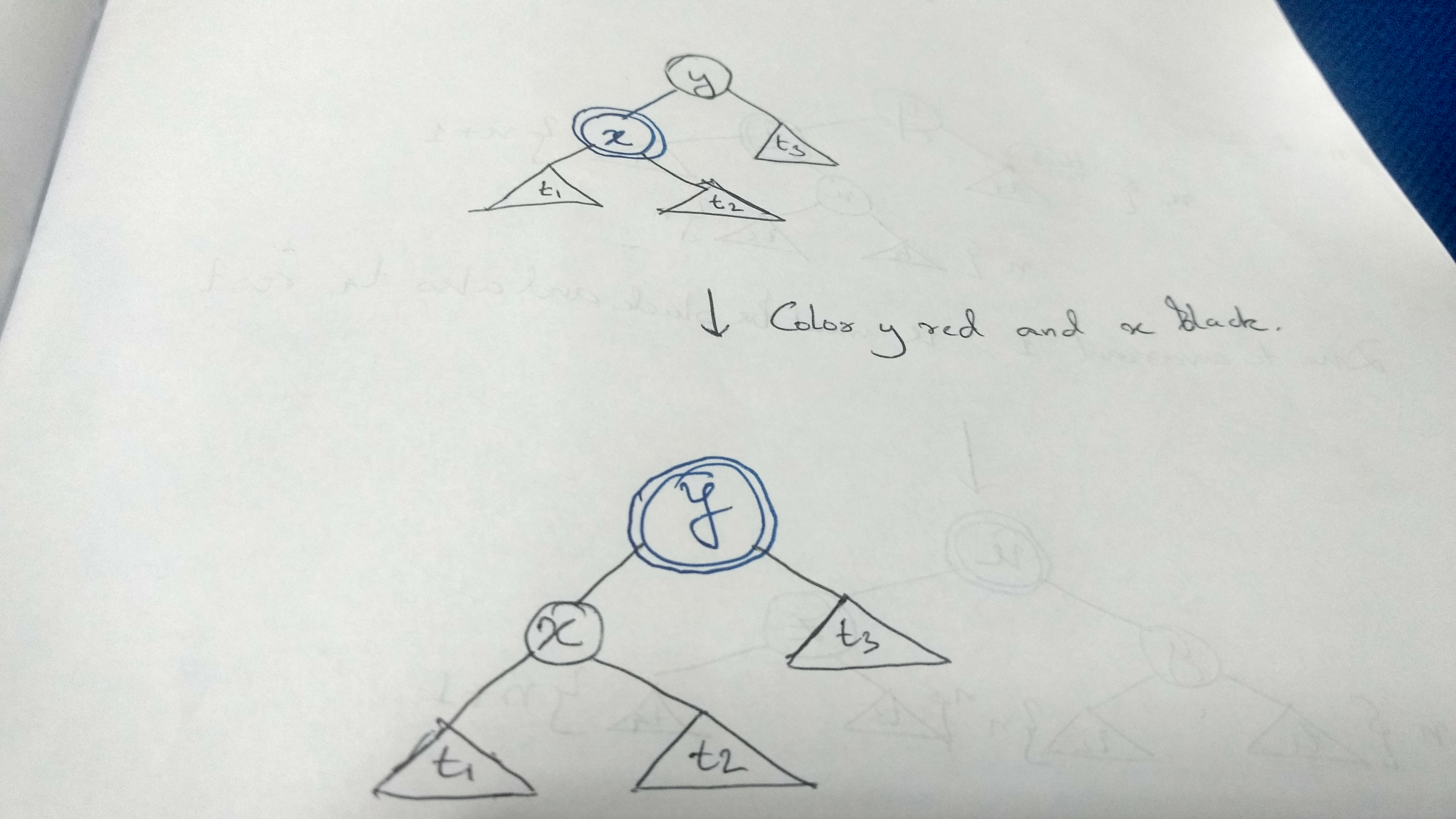
Coloring y red and x black we increase the height of left subtree by 1 and the height of the right subtree remains unchanged and hence it gets balanced. So translating the diagram to Haskell:

balL (T B (T R t1 x t2) y t3) = T R (T B t1 x t2) y t3

Case 2: Root node is black, left subtree root is black.

If the left subtree root is black we can’t touch the left tree as it is already shorter and altering the black node would shorten the height more. We need to look at the right subtree.

So depending on the color of the root node there are 2 subcases in this:

Case 2. i. Root node is black, right subtree root is black

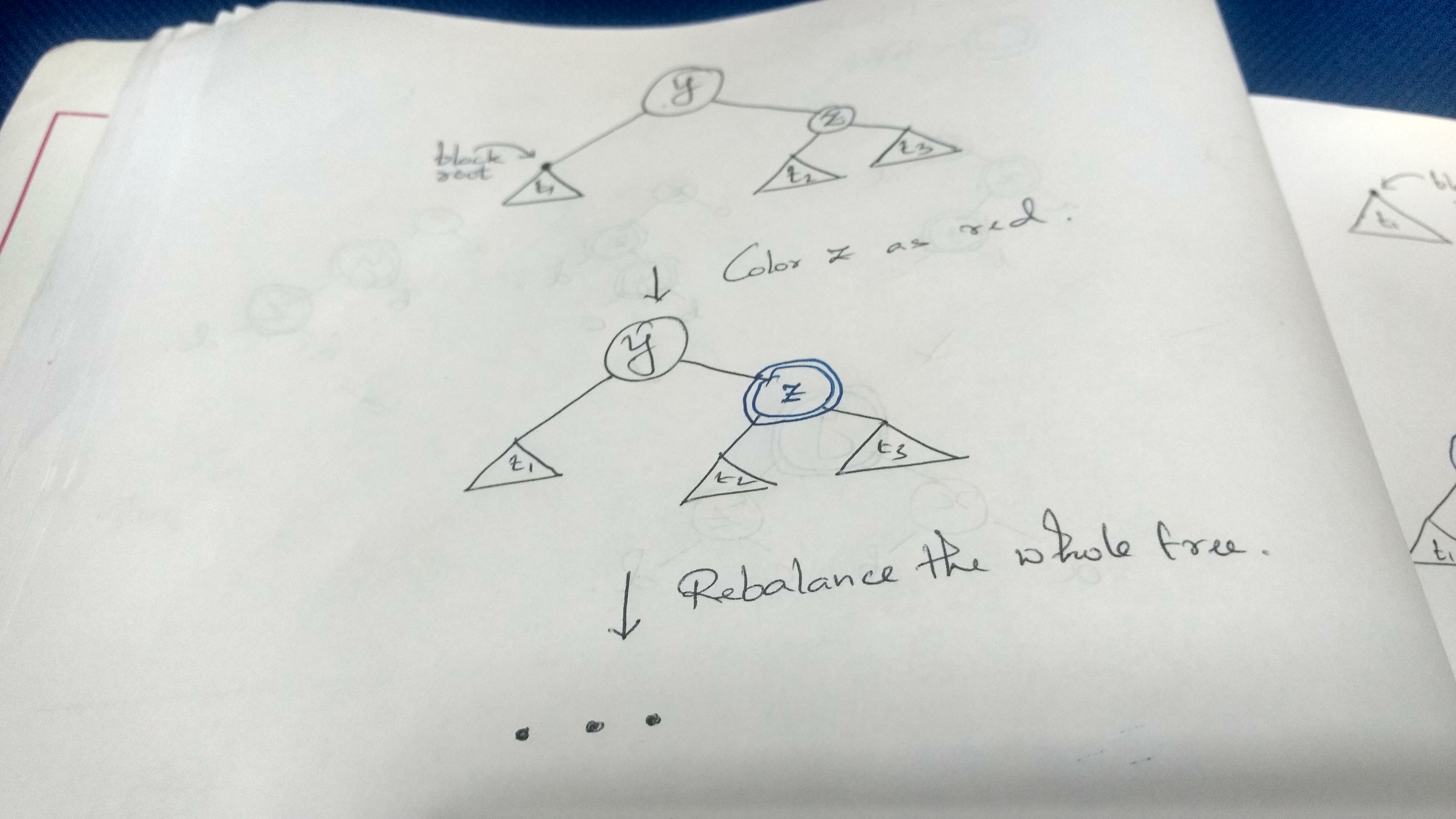
Coloring z as red reduces the height of the right subtree by 1 but it might end up violating invariant 1. In which case we have to call the old balance function that we used in case of invariant 1 violation. We can define a simple helper balance' which takes the entire node instead of passing the left subtree, right subtree, color etc. So this branch becomes:

balL (T B t1 y (T B t2 z t3)) = balance' (T B t1 y (T R t2 z t3))

Case 2. ii. Root node is black, right subtree root is red..

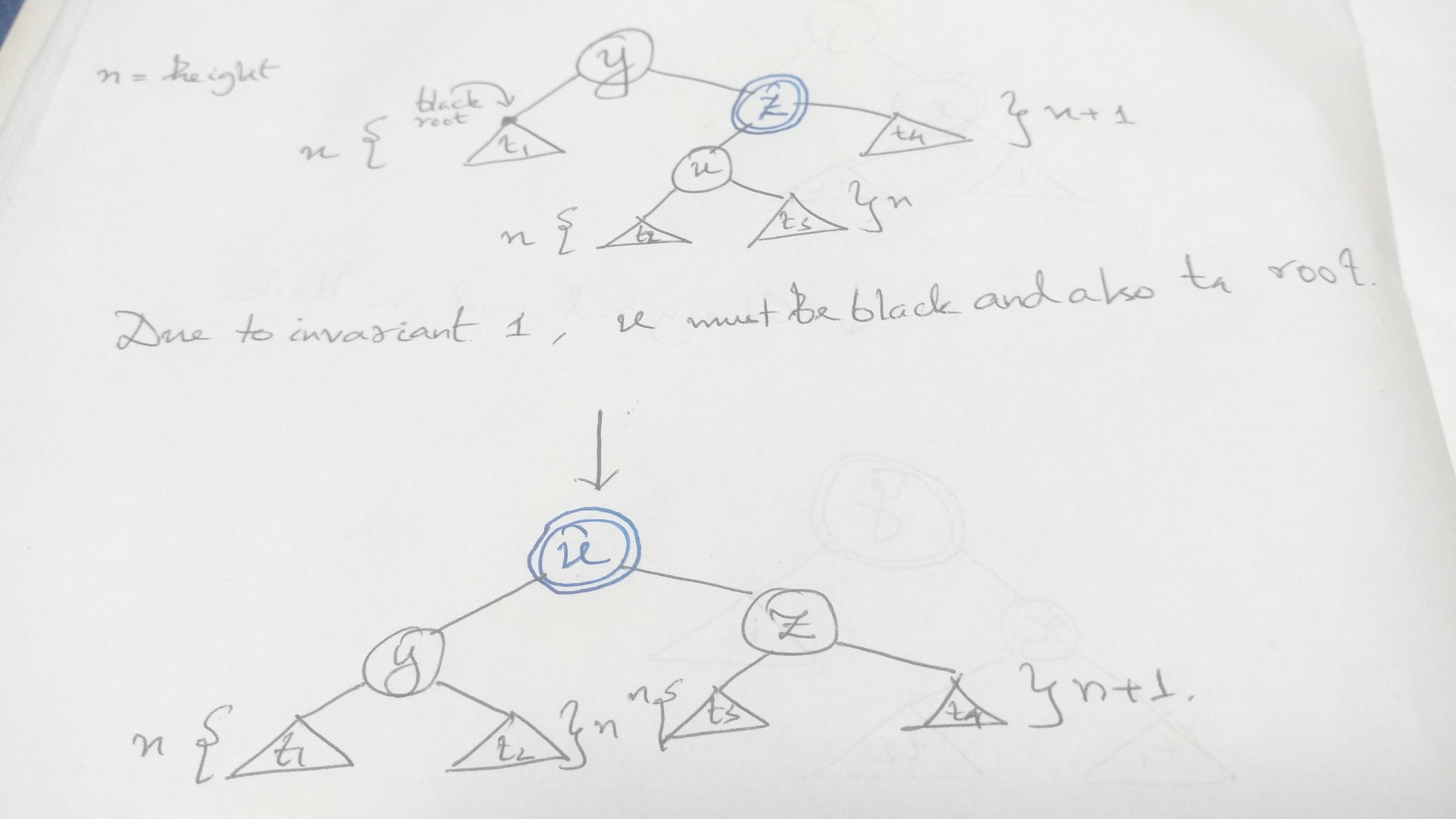
This is the most involved case. Here after rebalancing the tree the only issue is t4’s height is still n+1 which can be resolved by coloring its root red. However we need to rebalance the subtree of (t3 z t4) to resolve any violations of invariant 1.

Hence the code translates to:

balL (T B t1 y (T R (T B t2 u t3) z t4@(T B l value r))) =
  T R (T B t1 y t2) u (balance' (T B t3 z (T R l value r)))

This concludes our cases for balL. And balR is exactly symmetric to the cases of balL, except now the right subtree would be shorter. I am adding the code for that part just for reference.

balR :: Tree a -> Tree a
balR (T B t1 y (T R t2 x t3)) = T R t1 y (T B t2 x t3)
balR (T B (T B t1 z t2) y t3) = balance' (T B (T R t1 z t2) y t3)
balR (T B (T R t1@(T B l value r) z (T B t2 u t3)) y t4) =
  T R (balance' (T B (T R l value r) z t2)) u (T B t3 y t4)

Now that we have balL and balR sorted we can start thinking about the delL and delR function. The signature of these functions are simple enough, given a node and tree it returns a tree with that node removed:

delL :: (Ord a) => a -> Tree a -> Tree a

delR :: (Ord a) => a -> Tree a -> Tree a

So if you look at the cases of balancing above, balancing is required only when there is a black root node, in case the node is red we just recurse down the path. So the red case is simple:

delL x t@(T R t1 y t2) = T R (del x t1) y t2

delR x t@(T R t1 y t2) = T R t1 y (del x t2)

Now in case the root node is black we just balance the entire tree after the delete:

delL x t@(T B t1 y t2) = balL $ T B (del x t1) y t2

delR x t@(T B t1 y t2) = balR $ T B t1 y (del x t2)

And thats all, these are the possible cases of delL and delR.

So moving to the final case of the deletion, which is fusing the 2 subtrees when the node is found.

The cases are really simple when the color of 2 roots are different i.e. black and red or red and black.

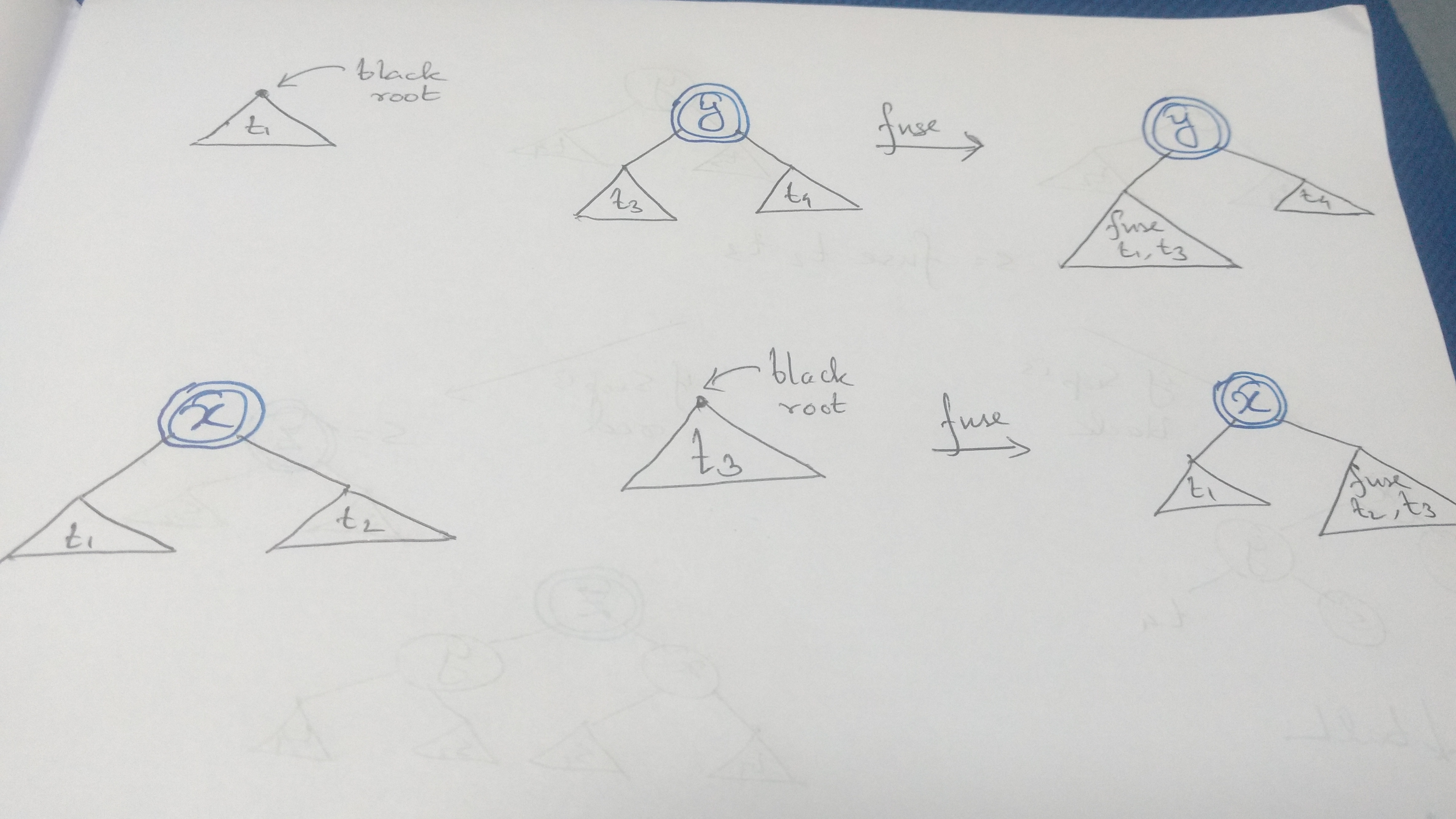
which again translates very easily to the code:

fuse t1@(T B _ _ _) (T R t3 y t4) = T R (fuse t1 t3) y t4
fuse (T R t1 x t2) t3@(T B _ _ _) = T R t1 x (fuse t2 t3)

The difficulty arises when the color of the roots are same.

Consider the case when both the roots are red:

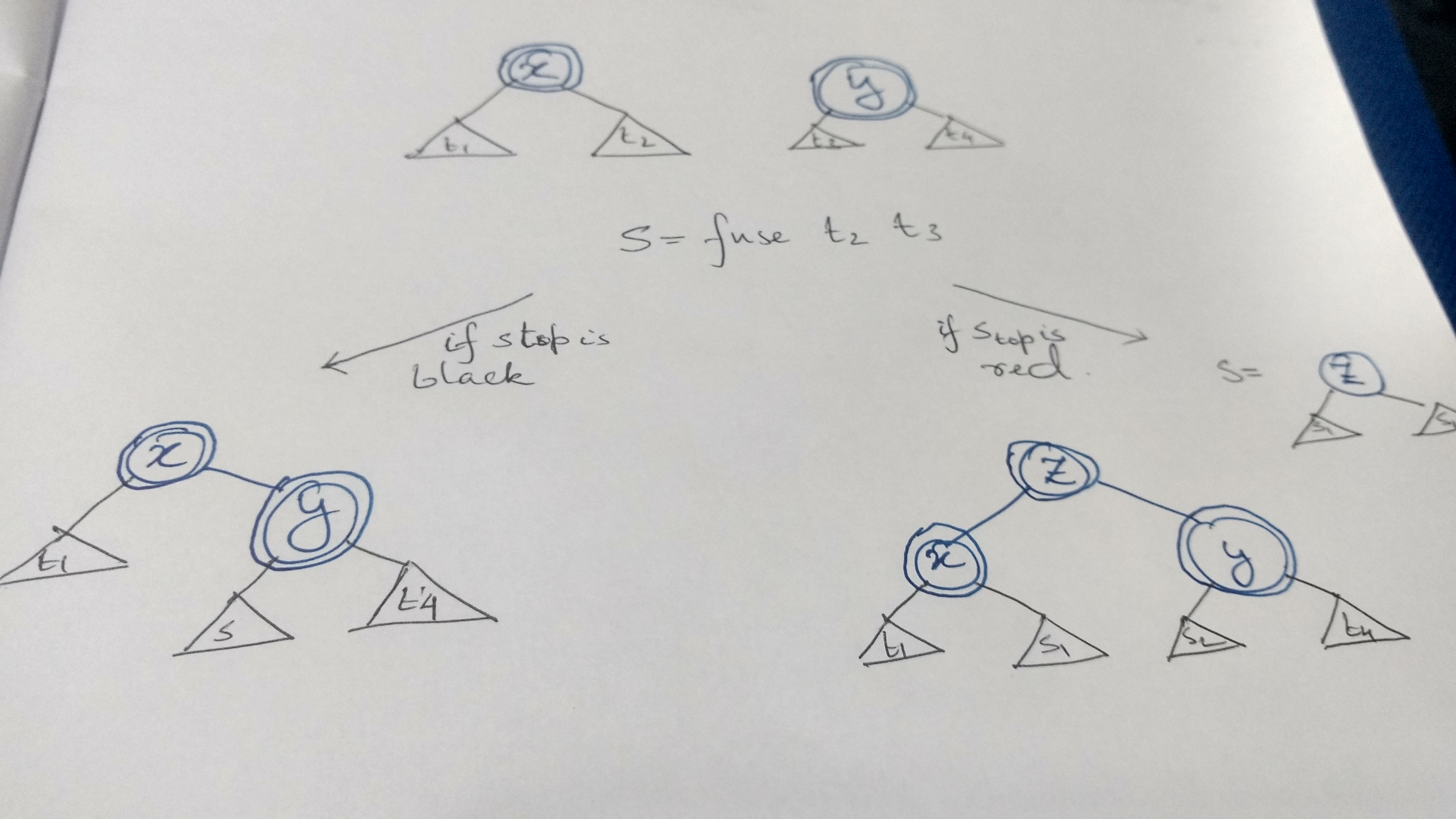
The transformation above are captured in the code below:

fuse (T R t1 x t2) (T R t3 y t4)  =
  let s = fuse t2 t3
  in case s of
       (T R s1 z s2) -> (T R (T R t1 x s1) z (T R s2 y t4))
       (T B _ _ _)   -> (T R t1 x (T R s y t4))

Any violation of invariant 1 is handled by the balance functions at the upper layers of the recursion.

Similarly the case when both roots are black:

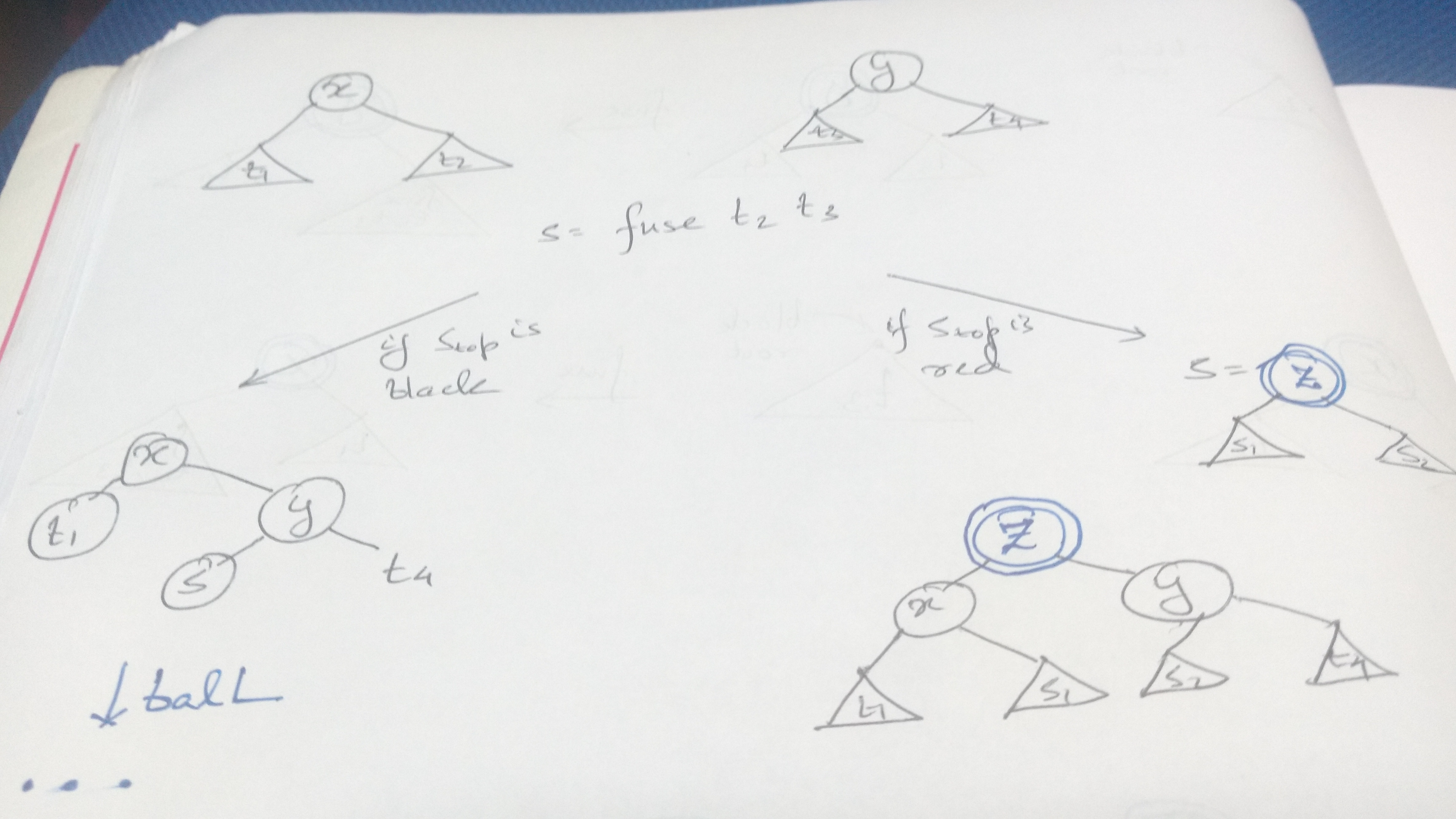
if the top node of s is black we need to use balL because the height of the right subtree has increased. And if it is red we follow the transformation given in the figure above:

fuse (T B t1 x t2) (T B t3 y t4)  =
  let s = fuse t2 t3
  in case s of
       (T R s1 z s2) -> (T R (T B t1 x s1) z (T B s2 y t4)) -- consfusing case
       (T B s1 z s2) -> balL (T B t1 x (T B s y t4))

Thats all. Putting together the entire code for delete we have:

delete :: (Ord a) => a -> Tree a -> Tree a
delete x t = makeBlack $ del x t
  where makeBlack (T _ a y b) = T B a y b
        makeBlack E           = E

del :: (Ord a) => a -> Tree a -> Tree a
del x t@(T _ l y r)
  | x < y = delL x t
  | x > y = delR x t
  | otherwise = fuse l r

delL :: (Ord a) => a -> Tree a -> Tree a
delL x t@(T B t1 y t2) = balL $ T B (del x t1) y t2
delL x t@(T R t1 y t2) = T R (del x t1) y t2

balL :: Tree a -> Tree a
balL (T B (T R t1 x t2) y t3) = T R (T B t1 x t2) y t3
balL (T B t1 y (T B t2 z t3)) = balance' (T B t1 y (T R t2 z t3))
balL (T B t1 y (T R (T B t2 u t3) z t4@(T B l value r))) =
  T R (T B t1 y t2) u (balance' (T B t3 z (T R l value r)))

delR :: (Ord a) => a -> Tree a -> Tree a
delR x t@(T B t1 y t2) = balR $ T B t1 y (del x t2)
delR x t@(T R t1 y t2) = T R t1 y (del x t2)

balR :: Tree a -> Tree a
balR (T B t1 y (T R t2 x t3)) = T R t1 y (T B t2 x t3)
balR (T B (T B t1 z t2) y t3) = balance' (T B (T R t1 z t2) y t3)
balR (T B (T R t1@(T B l value r) z (T B t2 u t3)) y t4) =
  T R (balance' (T B (T R l value r) z t2)) u (T B t3 y t4)

fuse :: Tree a -> Tree a -> Tree a
fuse E t = t
fuse t E = t
fuse t1@(T B _ _ _) (T R t3 y t4) = T R (fuse t1 t3) y t4
fuse (T R t1 x t2) t3@(T B _ _ _) = T R t1 x (fuse t2 t3)
fuse (T R t1 x t2) (T R t3 y t4)  =
  let s = fuse t2 t3
  in case s of
       (T R s1 z s2) -> (T R (T R t1 x s1) z (T R s2 y t4))
       (T B _ _ _)   -> (T R t1 x (T R s y t4))
fuse (T B t1 x t2) (T B t3 y t4)  =
  let s = fuse t2 t3
  in case s of
       (T R s1 z s2) -> (T R (T B t1 x s1) z (T B s2 y t4))
       (T B s1 z s2) -> balL (T B t1 x (T B s y t4))

The entire code is available here.

The above algorithm was first devised by Stefan Kahrs from University of Kent (Thanks to Dr. Venanzio Capretta for explaining the cases).There is an alternate red black deletion algorithm devised by Matt Might which uses auxiliary colors to simplify the cases. He has blogged about it in great detail here.

While the case of deletion is quite involved, if you take a look at the entire code for the red black tree, its hardly 100 lines of Haskell. And it is persistent in nature by default. It would be much more difficult designing a thread safe red black tree in any other imperative language. Most importantly, when teaching someone data structures for the first time, the syntax never intrudes in the way of the logic of the program. I have been working on this as part of a course on Advanced Data Structures and Algorithms that I am taking, and using Haskell has made understanding the logic dead simple.

Type Level Trees

In addition if we want, we can encode these invariants at the type level. Writing an entire type level Red Black Tree would require another post.

Stephanie Weirich from University of Pennsylvania has done lots of work in that area and there are many of her presentations available online.

As a small taste of what we can do, we can encode the simple invariant that “The difference in height between the 2 subtrees is maximum 1” to ensure that a BST is balanced. Fot that, what we need, is to raise a number to the type level and say that “if the height of left subtree is n then the height of the right subtree is either n + 1 or n - 1 and vice versa”.

We can represent numbers simply using Peano numerals. But first we need a couple of language extensions:

{-# LANGUAGE GADTs, DataKinds  #-}

Followed by that define the Peano numerals and capture the invariant in the tree:

data Nat = Zero | Succ Nat

data T n a = NodeR (Tree n a) a (Tree (Succ n) a) -- right subtree has height + 1
           | NodeL (Tree (Succ n) a) a (Tree n a) -- left subtree has height + 1
           | Node (Tree n a) a (Tree n a)     -- both subtrees are of equal height

data Tree n a where
  Branch :: T n a -> Tree (Succ n) a
  Leaf :: Tree Zero a

We can also raise relational operators to the type level using the singletons package by Richard Eisenberg and capture further invariants in the type level. But that will be material for another post. Till then enjoy writing more Haskell :)