Lenses and Optics

Purely functional references for traversals

Motivation

Promoting immutable programming.

Immutability simplifies a lot of concurrency woes.

However it makes working with certain data structures very difficult. Eg: Maps

Maps are ubiquitous.

• JSON
• OOP classes
• Haskell Records
• Caches
• Databases
• ..

Nearly everything useful you interact with has a map like API

Lets look at some problems working with Haskell records.

A very simple use case

data Person = P { name   :: String
                , addr   :: Address
                , salary :: Int
                }

data Address = A { road :: String
                 , city :: String
                 , postcode :: String}

Let us try to change the name of the person.

setName :: String -> Person -> Person
setName n P { name = n'
            , addr = a
            , salary = s}
  = P { name = n
      , addr = a
      , salary = s}

That was not bad!

Lets try to change his address

setPostcode :: String -> Person -> Person
setPostcode pc P { name = n
                 , addr = A { road = r
                            , city = c
                            , postcode = p}
                 , salary = s}
  = P { name = n
      , addr = A { road = r
                 , city = c
                 , postcode = pc}
      , salary = s}

This is starting to look ugly

A real world example from a medical site:

{
"problems": [{
    "Diabetes":[{
        "medications":[{
            "medicationsClasses":[{
                "className":[{
                    "associatedDrug":[{
                        "name":"asprin",
                        "dose":"",
                        "strength":"500 mg"
                    }],
                    "associatedDrug#2":[{
                        "name":"somethingElse",
                        "dose":"",
                        "strength":"500 mg"
                    }]
                }],
                "className2":[{
                    "associatedDrug":[{
                        "name":"asprin",
                        "dose":"",
                        "strength":"500 mg"
                    }],
                    "associatedDrug#2":[{
                        "name":"somethingElse",
                        "dose":"",
                        "strength":"500 mg"
                    }]
                }]
            }]
        }],
        "labs":[{
            "missing_field": "missing_value"
        }]
    }],
    "Asthma":[{}]
}]}

To change the strength of a medicine, which is buried 6 level deep, we have to reconstruct the entire record.

This will cost you the entire reconstruction time and space!!

Don't even bother trying!!

Introducing Lens

Hassle free data traversals à la Edward Kmett

The Hack

(.) in Java acts as an accessor

employee.setAddress.setPostcode("NG7 2AW")

(.) in Haskell acts as function composition

(.) :: (b -> c) -> (a -> b) -> a -> c

Lens composes functions in a way, that presents a seemingly MUTABLE API, for immutable programming, via the magic of function composition

Let's try to build a basic Lens type

A Lens primary comprises of 3 functions

• view
• set
• modify

view

Given a structure we want to view or "focus" on a particular part of the structure

set

Given a particular value to be set and a structure we want to create a new structure with that value set

modify

Given a function to modify a part of the structure we want to apply that function to the part of the structure and return the structure

Lets write the types!

data LensR s a
  = L { view   :: s -> a
      , set    :: a -> s -> s
      , modify :: (a -> a) -> s -> s
      }

What about IO interactions?

data LensR s a
  = L { view     :: s -> a
      , set      :: a -> s -> s
      , modify   :: (a -> a) -> s -> s
      , modifyIO :: (a -> IO a) -> (s -> IO s)
      }

What about interactions which can fail?

data LensR s a
  = L { view     :: s -> a
      , set      :: a -> s -> s
      , modify   :: (a -> a) -> s -> s
      , modifyIO :: (a -> IO a) -> (s -> IO s)
      , modifyM  :: (a -> Maybe a) -> (s -> Maybe s)
      }

What about stateful interactions?

data LensR s a
  = L { view     :: s -> a
      , set      :: a -> s -> s
      , modify   :: (a -> a) -> s -> s
      , modifyIO :: (a -> IO a) -> (s -> IO s)
      , modifyM  :: (a -> Maybe a) -> (s -> Maybe s)
      , modifyS  :: (a -> State s a) -> (s -> State s s)
      }

Can you notice a pattern?

Every interaction is falling into this pattern

modifyFoo :: (a -> Foo a) -> (s -> Foo s)

And if you really squint your eyes:

set :: a -> s -> s

view is the only function whose types do not visibly seem similar

Let us try to capture the entire pattern using one function excluding view

type Lens f s a = (a -> f a) -> (s -> f s)

A short digression

Jargon time

• Higher Rank Polymorphism
• Functors

Constraints liberate. Liberties constrain.

Eg:

foo :: Num a => a -> a    foo :: Bool a => a -> a
foo 5 = 6                 foo True  = False
foo 6 = 8                 foo False = True
foo ...                   foo ...

Now lets liberate the type level

foo :: forall a . a -> a
foo x = x

Functors

A functor is a Higher Kinded Type

class Functor f where
  fmap :: (a -> b) -> f a -> f b

Higher kinded types take one or more types and return a type.

IO, Maybe, State are all monads.

But all monads are functors.

Functors are weaker than monads but they have laws

fmap id = id
fmap (f . g) = fmap f . fmap g

Back to lens

Lets combine higher rank polymorphism and functors

Van Laarhoven Lens

One function to rule them all

type Lens s a = forall f . Functor f => (a -> f a) -> (s -> f s)

Claim: view, set and modify are all captured by this function.

Lets look at view

view :: s -> a

type Lens s a = forall f . Functor f => (a -> f a) -> (s -> f s)

Seriously? How on earth?

Say hello to the Const type

newtype Const v a = Const v

getConst :: Const v a -> v
getConst (Const x) = x

instance Functor (Const v) where
  fmap f (Const x) = Const x

view :: forall s a . Lens s a -> s -> a
view ln s = ?

λ> :t Const
Const :: v -> Const v a

Remember:

type Lens s a = forall f . Functor f => (a -> f a) -> (s -> f s)

Now,

(a -> f a) ≡ Const ≡ (a -> Const a a)
s ≡ s

So

ln Const s ≡ Const a s

Hence

view :: forall s a . Lens s a -> s -> a
view ln s = getConst  $ ln Const s

Similarly,

Using the identity functor we can get

set :: forall s a . Lens s a -> a -> s -> s
set ln x s = runIdentity $ ln (\_ -> Identity x) s

modify :: forall s a . Lens s a -> (a -> a) -> s -> s
modify ln f s = runIdentity $ ln (Identity . f) s

LENSES COMPOSE!!

Because it is just a function

Remember the old medical site example

Lets compose our way into its depth:

Lens Problem Disease .
Lens Disease Medication .
Lens Medication MedicationClass .
Lens MedicationClass Classname .
Lens Classname Drug .
Lens Drug String
 = Lens Problem String

That was just plain old function composition!

And making a Lens can be incredibly automated

import Control.Lens.TH

$(makeLenses ''Problem)
$(makeLenses ''Disease)
$(makeLenses ''Medication)
...

And if you don't like metaprogramming

Generalizing the Lens type

type Lens s t a b = forall f . Functor f => (a -> f b) -> s -> f t

Is that all?

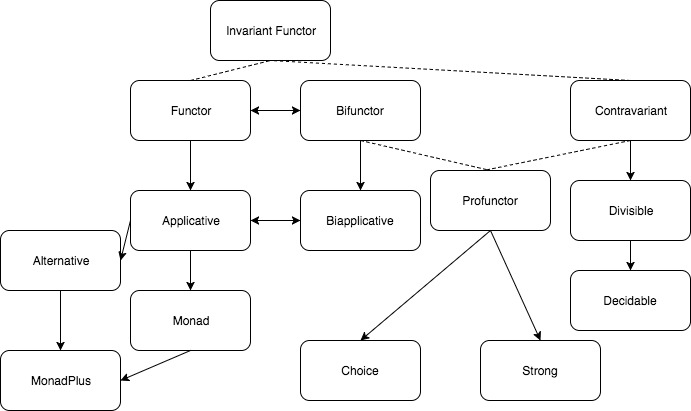
How big is the functor family?

The functor hierarchy existing in Haskell excluding lots of interesting categories

Constraining this in various ways

type Lens s t a b = forall f . (??) => (a -> f b) -> s -> f t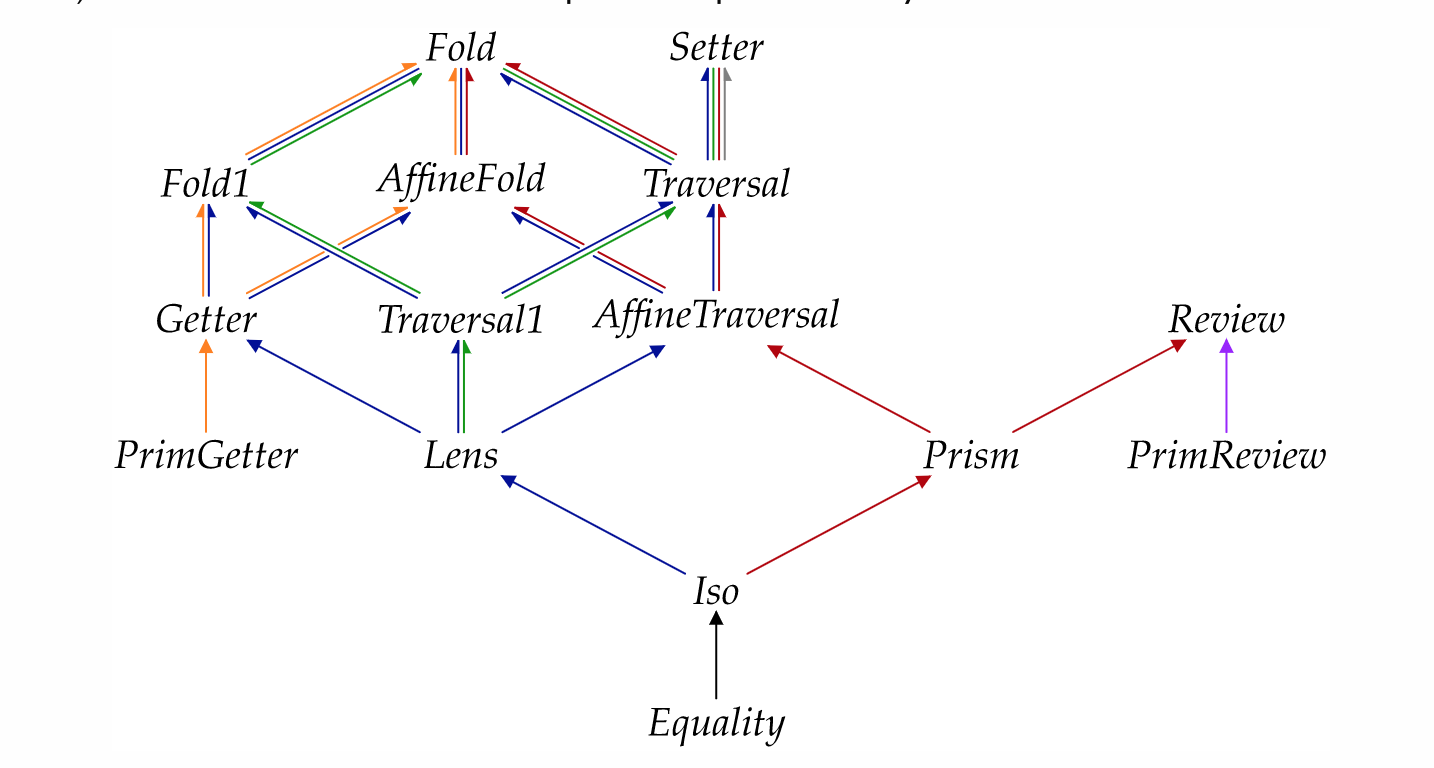

But thats too much jargon for my taste!

Edward Kmett on Haskell reddit

Lets talk performance

Lens inlines aggresively

Inlining example from SPJ's talk

view :: Lens s a -> (s -> a)
view ln = getConst . ln Const

 -- Template Haskell generated
name :: Lens Problem String
name elt_fn (P n s)
  = fmap (\n' -> P n' s) (elt_fn n)

view name (P {_name = "Fred", _salary = 100})
 -- inline view
= getConst (name Const (P {_name = "Fred"}))
 -- inline name
= getConst (fmap (\n' -> P n' 100) (Const "Fred"))
 -- fmap f (Const x) = Const x
= getConst (Const "Fred")
 -- getConst (Const x) = x
= "Fred"

view, set and modify inlines almost everything

Giving O(1) time complexity

Same as Java, C++ accessors

But the actual win is in space complexity!

A normal map implementation would have linear space growth

Inlining leads to O(1) space complexity for updates in persistent data structures

Traversals can be parallelized for free

type Traversal s t a b = forall f . Applicative f => (a -> f b) -> (s -> f t)

Monad = sequential

Applicative = parallel

Time Complexity O(1) but faster on multiple cores

This is the tip of the iceberg:

• Profunctor Optics

• Indexed Optics

• ...

Example of how crazy it can get:

Entire code up on github

https://github.com/Abhiroop/opto

Future work will be based on this:

References

Special Thanks to

Prof. Jeremy Gibbons,

for clarifying my doubts over the mail on a Sunday

Others:

Edward Kmett, NYC Haskell Meetup Talk

Simon Peyton Jones, Haskell Exchange 2013

Blog post series by Jakub Arnold https://blog.jakuba.net