Hello (Hej!)
I am Abhiroop!
MASTERS THESIS
Superword Level Parallelism in the Glasgow Haskell Compiler
Single Instruction Multiple Data
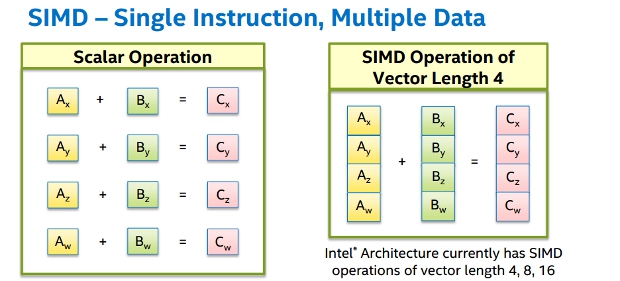
Motivation
- Power efficient
- Lesser FDE cycles for a given data size
- ML algorithms are data parallel in nature
- Numerical computing algorithms are data parallel
OUTCOMES
- Support for SSE and AVX instructions in the NCG of GHC (Float and Double)
- Some core changes in
Data.Int - Flat Data Parallelism over SIMD registers in GHC (https://github.com/Abhiroop/lift-vector)
FAILURES
- Automatic Vectorization
ghc -ftree-vectorize Program.hs
State of the art in LLVM : Porpodas, Vasileios, and Timothy M. Jones. "Throttling automatic vectorization: When less is more."
POSSIBLE DIRECTIONS
- Experiment with SSA representation inside GHC
- Explore the SPMD on SIMD approach
Today's Talk:
Parallelizing Cons List*
(and a few incomplete optimization stories)
CONS LIST
- car (head)
- cdr (tail)
- cons
cons (car xs) (cdr xs) = xs
Cons List are sequential by construction

length operation:
length :: [a] -> Int
length [] = 0
length (x:xs) = 1 + length xsThis is a parallelizable operation
if we had,
length :: [a] -> Int
length [] = 0
length [a] = 1
length (a ++ b) = length a + length bGuy Steele - ICFP 2009
"foldl and foldr considered slightly harmful"
We must lose the “accumulator” paradigm and emphasize “divide-and-conquer”.
CONC LISTS
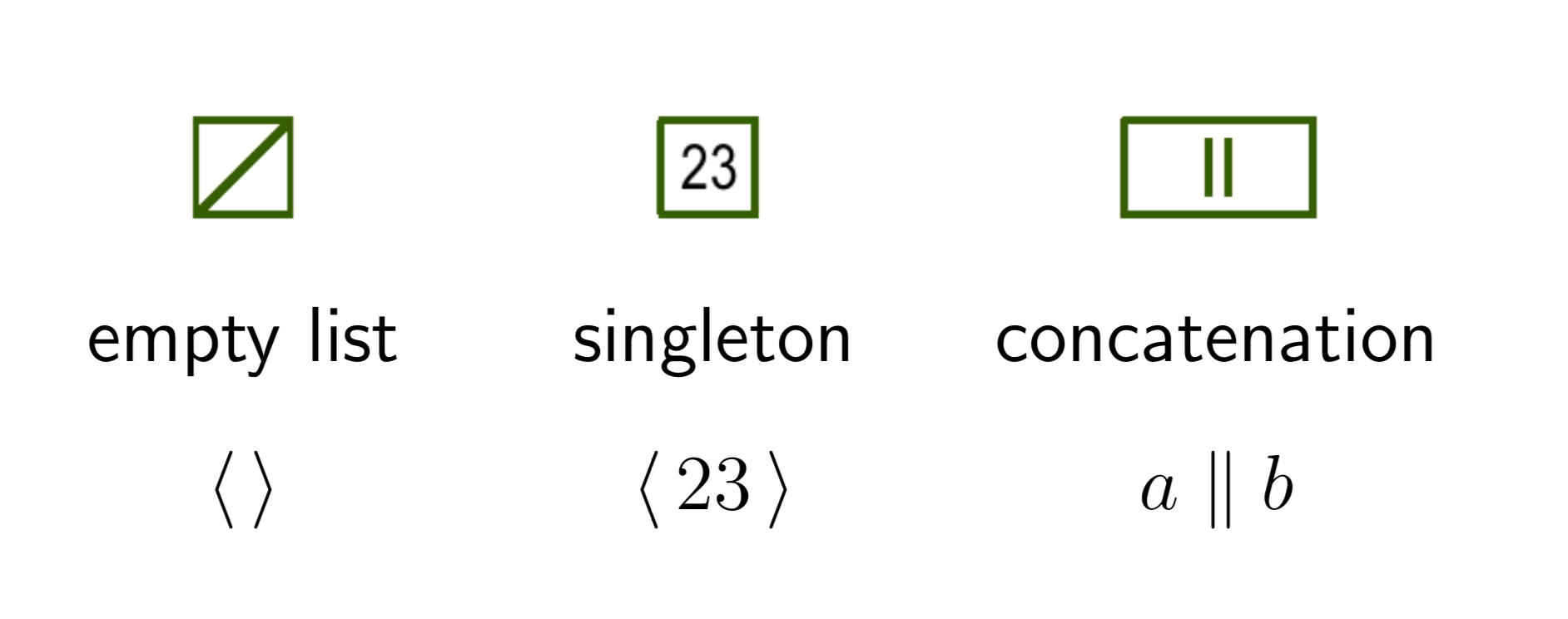
Introduced by Guy Steele in Fortress
Conc List implementations available in
- Fortress
- Scala
This talk is about a conc-list implementation in Haskell
Simple inductive structure
data List a =
Empty
| Singleton a
| Conc (List a) (List a)length :: List a -> Int
length Empty = 0
length (Singleton a) = 1
length (Conc xs ys)
= length xs + length ys -- potentially parallelizableWhat happens when you filter?
filter :: (a -> Bool) -> List a -> List a
filter _ Empty = Empty
filter p (Singleton x)
| p x -> (Singleton x)
| otherwise -> Empty
filter p (Conc xs ys) = Conc (p xs) (p ys)let l =
Conc
(Conc (Singleton 23)
(Singleton 47))
(Conc (Singleton 18)
(Singleton 11))
filter (x > 15) l
=> Conc
(Conc (Singleton 23)
(Singleton 47))
(Conc (Singleton 18)
Empty)Conc lists allow multiple possible represrentations of the same list
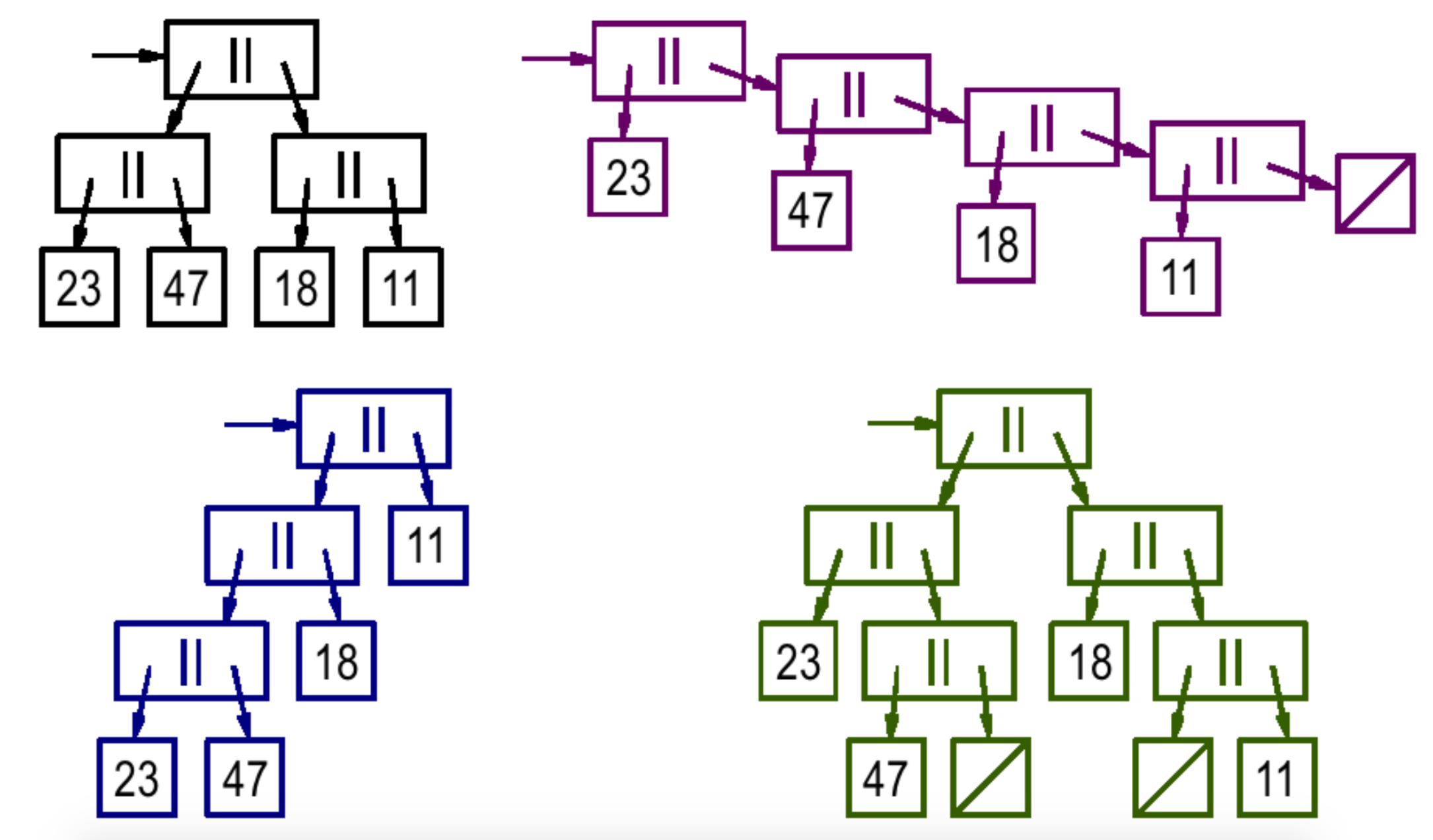
Operations like filter spoil the "divide and conquer" like quality of the structure
We need a balanced tree.
type List a = Tree a
data Color = R | B deriving Show
data Tree a
= E
| S a
| C Color (Tree a) (Tree a)insert on an RB Tree is quite simple.
delete is quite complex.
The core API: cons, car, cdr
cons :: Ord a => a -> List a -> List a
cons = insert
head :: List a -> Maybe a
head E = Nothing
head (S x) = Just x
head (C _ l _) = head l
tail :: Ord a => List a -> Maybe (List a)
tail E = Nothing
tail (S x) = Nothing
tail (C _ l r)
= let left_tail = fromMaybe E (tail l)
in Just $ conc left_tail rconc is slightly tricky
conc :: Ord a => List a -> List a -> List a
conc E E = E
conc E (S a) = S a
conc E (C c l r) = C c l r
conc (S a) E = S a
conc (S a) (S b) = insert a (S b)
conc (S a) (C c l r) = insert a (C c l r)
conc (C c l r) E = C c l r
conc (C c l r) (S a) = balance B (C c l r) (S a)
conc (C c1 l1 r1) (C c2 l2 r2) = balance B (C c1 l1 r1) (C c2 l2 r2)
-- final implementation makes conc O(log n)And also,
type List a = Tree a
instance Ord a => Semigroup (List a) where
(<>) = conc
instance Ord a => Monoid (List a) where
mempty = E
mappend = (<>)conc (left xs) (right xs) = xs
Instead of implementing every function from Prelude in a specific way lets implement a general function.
foldMap :: Monoid m
=> (a -> m)
-> List a -- the actual structure
-> m
foldMap _ E = mempty
foldMap f (S x) = f x
foldMap f (C _ ys zs) = mappend (foldMap f ys) (foldMap f zs)
length = getSum . foldMap (\_ -> Sum 1)
map f xs = foldMap (\x -> S (f x)) xs
filter p = foldMap (\x -> if p x then (S x) else E)
fold = foldMap idHow do we parallelize the operations?
foldMap :: Monoid m
=> (a -> m)
-> List a -- the actual structure
-> m
foldMap _ E = mempty
foldMap f (S x) = f x
foldMap f (C _ ys zs) = par2 mappend (foldMap f ys) (foldMap f zs)
par2 :: (a -> b -> c) -> a -> b -> c
par2 f x y = x `par` y `par` f x ypar is the simplest way to write pure parallel operations
par :: a -> b -> b
par x y = case (par# x) of { _ -> lazy y }What is the problem with this?
- Task granularity too small
(<>) = concis too costly
We need to restrict the parallelism
HEIGHT ANNOTATED RED BLACK TREE
data Tree a
= E
| S a
| C {-# UNPACK #-} !Height
!Color
!(Tree a)
!(Tree a)Now we can restrict the parallelism
foldMap :: Monoid m
=> (a -> m)
-> List a -- the actual structure
-> m
foldMap f t@(C h' _ _ _) = go t (h' - (logBase 2 h'))
where
go E _ = mempty
go (S x) _ = f x
go (C h _ ys zs) parallelDepth
| h >= parallelDepth = gol `par` gor `par` mappend gol gor
| otherwise = mappend gol gor
where
gol = go ys (n + 1)
gor = go zs (n + 1)A more sensible parallelDepth magnitude
Plot a graph between performance and depth of throttling the parallelism
Can suggest a correlation between the two
JITed runtimes play with this sort of numbers
If we dynamically accept the mappend function
foldMap' :: (a -> m)
-> (m -> m -> m)
-> m
-> List a -- the actual structure
-> m
foldMap' f g unit t@(C h' _ _ _) = go t (h' - (logBase 2 h'))
where
go E _ = unit
go (S x) _ = f x
go (C h _ !ys !zs) parallelDepth
| h >= parallelDepth = gol `par` gor `par` g gol gor
| otherwise = g gol gor
where
gol = go ys (n + 1)
gor = go zs (n + 1)We can reverse in parallel
reverse :: Ord a => List a -> List a
reverse = foldMap' S (\ys zs -> conc zs ys) EADVANTAGES
SHORTCOMINGS
- Space usage (for 10 million elements)
Height annotated RB Trees
16,554,468,768 bytes allocated in the heap
2,715,002,064 bytes copied during GC
615,645,336 bytes maximum residency (12 sample(s))
1,494,888 bytes maximum slop
1204 MB total memory in use (0 MB lost due to fragmentation)Lists
720,127,264 bytes allocated in the heap
1,069,984 bytes copied during GC
95,992 bytes maximum residency (2 sample(s))
55,560 bytes maximum slop
5 MB total memory in use (0 MB lost due to fragmentation)- List Fusion still more efficient
> length [0..10_000_000]
Rec {
lim_r3Bl = 10000000
lvl_r3Bm = 1
Foo.$wgo :: Integer -> GHC.Prim.Int# -> GHC.Prim.Int#
Foo.$wgo
= \ w_s3Ax ww_s3AB ->
case gtInteger# w_s3Ax lim_r3Bl
of {
__DEFAULT ->
Foo.$wgo
(plusInteger w_s3Ax lvl_r3Bm) (+# ww_s3AB 1#);
1# -> ww_s3AB
}
end Rec }POSSIBLE IMPROVEMENTS
- Increase the branching factor
Eg: Clojure's persistent lists have a branching factor of 32
-- A conc-rose tree
data NTree a
= E
| S a
| C !Height [NTree a]CONCLUSION
“To make the program faster, we have to gain more from parallelism than we lose due to the overhead of adding it, and compile-time analysis cannot make good judgments in this area.” - Simon Marlow
Pessimistic estimations of task granularity
Runtime profile aided parallelism