Declarative Vector Programming

Abhiroop Sarkar

OUTLINE

Motivation
My Master's Thesis
Lift-Vector : A library for vector programming
An alternate programming model?
Automatic Vectorization (if time permits)

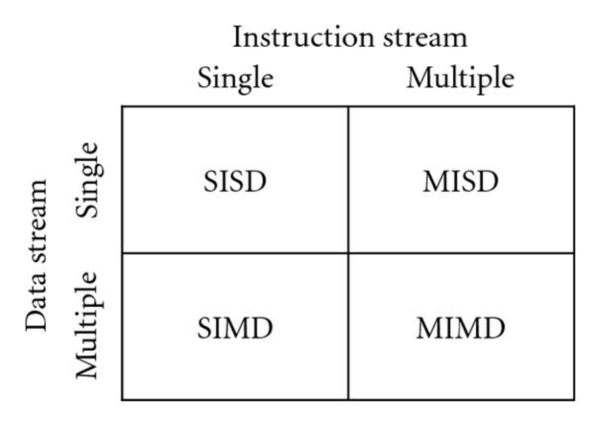
Types of Parallel Machines

Flynn

Single Instruction Multiple Data

Simd

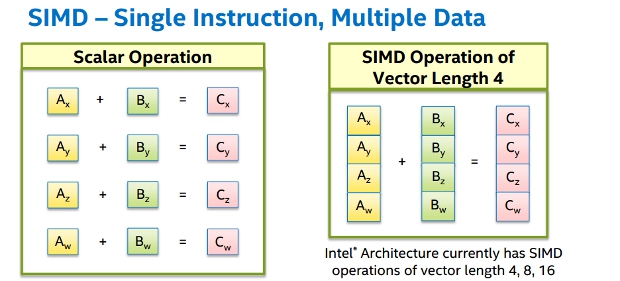
WHY SIMD?

Power efficient
Relative low cost in die area
Lesser FDE cycles for a given data size
ML algorithms are data parallel in nature
Numerical computing algorithms are data parallel

cvg

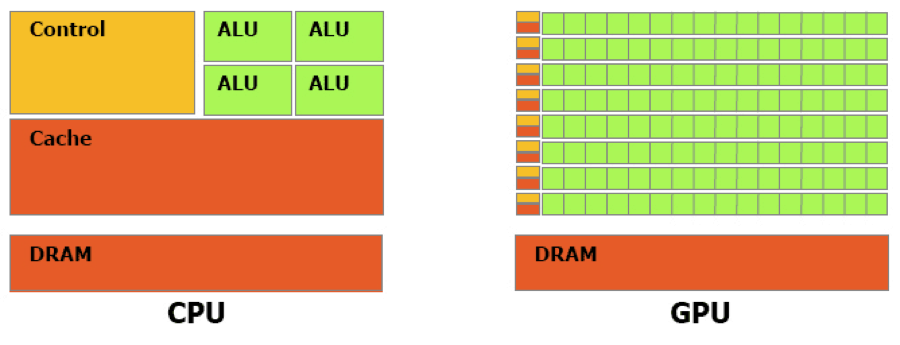
We focus on CPU vector programming.

More flexible memory model compared to GPUs
Easier to implement stack and recursion in CPUs
GPU data transfer bandwidth capped at 15 GB/s

x86 Instruction Set

Intel
- SSE (Intel P6, 1999)
- SSE2 (Intel Pentium M, 2003)
- SSE3 (NetBurst - Pentium 4, 2004)
- SSE4.1 (Intel Core, 2006)
- SSE4.2 (Nehalem, 2008)
- AVX (SandyBridge, 2011)
- AVX2 (Haswell, 2013)
- AVX512 (Canon Lake, 2018)
AMD

Compiler Support

GCC
LLVM Toolchain
Dyalog APL

Software Support

OpenMP
OpenCL

Can a purely functional language support vectorisation?

Enriching the question...

Can a purely functional language support vectorisation, preserving its original syntax and semantics while being as efficient as low level systems programming languages?

We will attempt to answer this throughout the rest of the presentation

MASTER'S THESIS

Superword Level Parallelism in the Glasgow Haskell Compiler

We will avoid talking about the engineering aspects and try to focus on the research side of the problem.

ghcpipe

Float supports FloatX4, a vector data type

Double supports DoubleX2, a vector data type

The user-level API

 -- constructors
packFloatX4#      :: (# Float#, Float#, Float#, Float# #) -> FloatX4#
broadcastFloatX4# :: Float# -> FloatX4#
 -- destructors
unpackFloatX4# :: FloatX4# (# Float#, Float#, Float#, Float# #)
 -- operations
plusFloatX4#   :: FloatX4# -> FloatX4# -> FloatX4#
minusFloatX4#  :: FloatX4# -> FloatX4# -> FloatX4#
timesFloatX4#  :: FloatX4# -> FloatX4# -> FloatX4#
divideFloatX4# :: FloatX4# -> FloatX4# -> FloatX4#

SSE as well as AVX support

Example : Vectorizing dot product

This spoils the declarative nature of Haskell!

Lift-Vector

Polymorphic SIMD functions for vector programming

Lift-vector provides two interfaces

Data.Primitive
Data.Operations

Data.Primitive

class (Num v, Real (Elem v)) => SIMDVector v where
    type Elem v

    type ElemTuple v

    nullVector       :: v
    vectorSize       :: v -> Int
    elementSize      :: v -> Int
    broadcastVector  :: Elem v -> v
    mapVector        :: (Elem v -> Elem v) -> v -> v
    zipVector        :: (Elem v -> Elem v -> Elem v) -> v -> v -> v
    foldVector       :: (Elem v -> Elem v -> Elem v) -> v -> Elem v
    sumVector        :: v -> Elem v
    packVector       :: ElemTuple v -> v
    unpackVector     :: v -> ElemTuple v

Data.Operations

class (Num a, Num b) =>
      ArithVector t a b
  where
  -- | The folding function should be commutative.
  fold :: (a -> a -> a) -> (b -> b -> b) -> b -> t b -> b
  zipVec ::
       (a -> a -> a) -> (b -> b -> b) -> t b -> t b -> t b
  fmap  :: (a -> a) -> (b -> b) -> t b -> t b
  -- | Work efficient Blelloch Scan
  scanb :: (a -> a -> a) -> (b -> b -> b) -> b -> t b -> t b

Vectorised Containers

Vector Lists
Vector Arrays (Shape polymorphic)

Vector Lists

newtype VecList a = VecList [a]

A wrapper over plain lists

Vector Arrays

Wrappers around unboxed vectors.

unboxed


import qualified Data.Vector.Unboxed as U

data VecArray sh a = VecArray !sh (U.Vector a)

What does dot product look like with the parallel operators?

Vector Lists

dotVec :: [Float] -> [Float] -> Float
dotVec xs ys =
  fold (\x y -> x + y :: FloatX4) (\x y -> x + y :: Float) 0 $
  zipVec
    (\x y -> x * y :: FloatX4)
    (\x y -> x * y :: Float)
    (toVecList xs)
    (toVecList ys)

Vector Arrays

dotVec' :: [Float] -> [Float] -> Float
dotVec' xs ys
 = let l1 = length xs
       l2 = length ys
    in fold (\x y -> x + y :: FloatX4) (\x y -> x + y :: Float) 0 $
       zipVec
        (\x y -> x * y :: FloatX4)
        (\x y -> x * y :: Float)
        (toVecArray (Z :. l1) xs)
        (toVecArray (Z :. l2) ys)

How are the Data.Operations operators implemented?

ZIP

zip

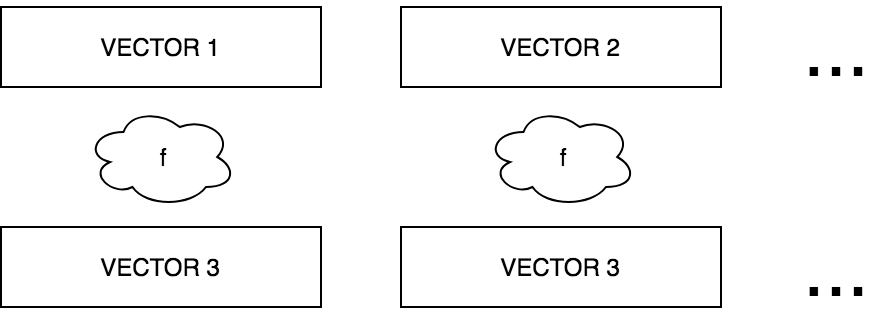
MAP

map

FOLD

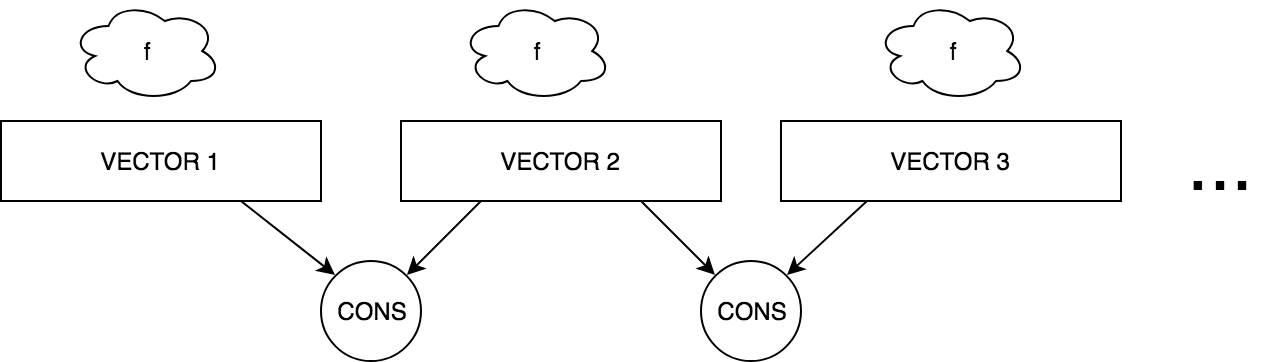
fold

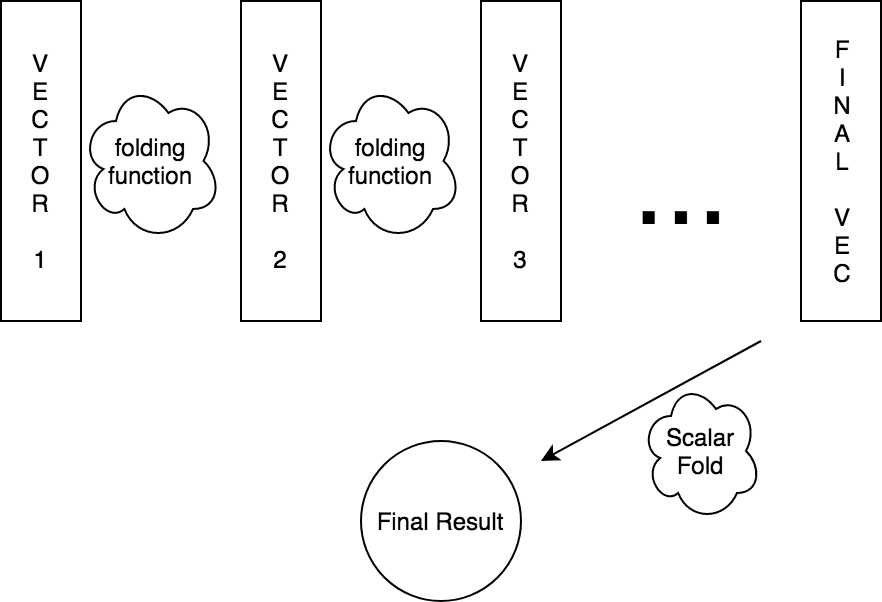
SCAN

scan or prefix sum looks like an inherently sequential operation

> scanl (+) 0 [1, 2, 3, 4, 5, 6, 7, 8]
> [0,1,3,6,10,15,21,28,36]

Lift-vector supports a work efficient parallel scan

BLELLOCH SCAN

UPSWEEP

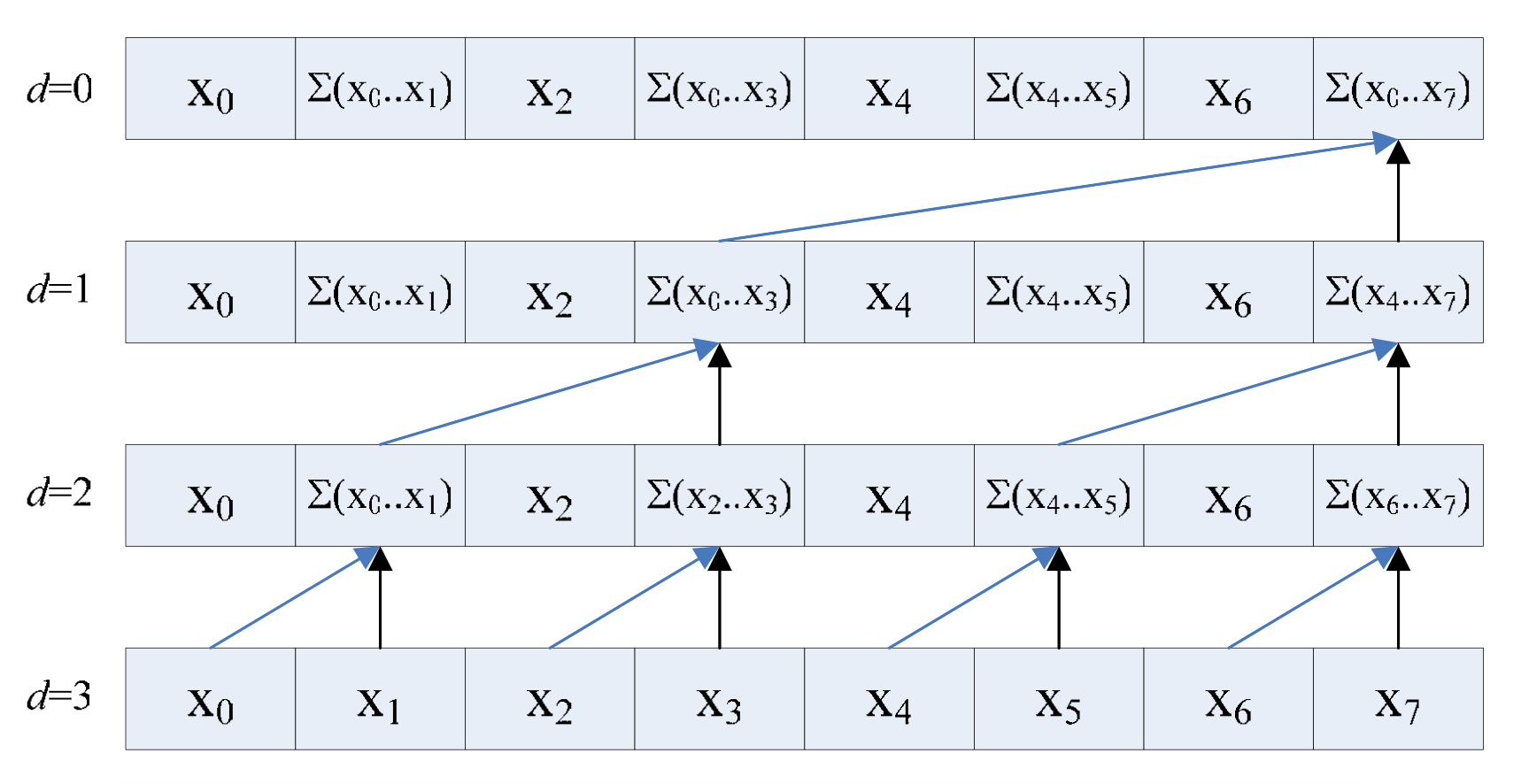
upsweep

DOWNSWEEP

downsweep

Benchmarks

Good benchmarks

Heavy reads and less write

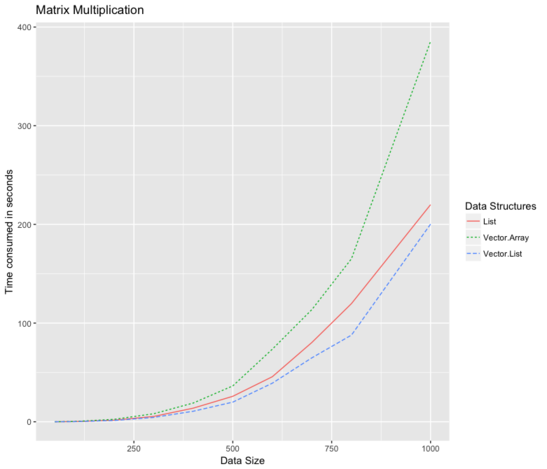
Pearson Correlation Coefficient

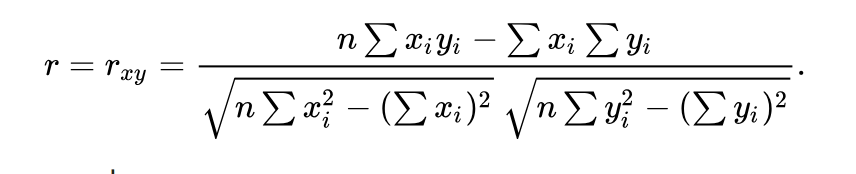
coeff

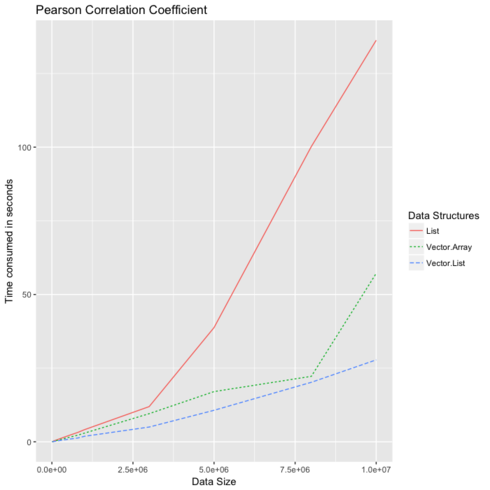
pearson

Bad benchmarks

Heavy writes

Eg: Matrix Multiplication

mmult

Lift Vector

https://github.com/Abhiroop/lift-vector

DISADVANTAGES OF LIFT-VECTOR

Leaky abstraction
Supports just flat and regular data parallelism
No focus on optimizing memory layout
Number of rewrite opportunities missed
...

EXAMPLE

import qualified Data.Operations as Op

foo :: Float -> Float
foo x = x*x + 1

foo' :: [Float] -> [Float]
foo' xs =
  Op.fromVecList $
  Op.fmap (\x -> x + 1 :: Float) (\x -> x + 1 :: FloatX4) $ 
  Op.fmap (\x -> x * x :: Float) (\x -> x * x :: FloatX4) $
  Op.toVecList xs

Any calls to map foo should be replaced by foo'

Now,

bar :: [Float] -> [Float]
bar xs = map foo xs

bar :: [Float] -> [Float]
bar = foo'

bar' :: [[Float]] -> [[Float]]
bar' xss = ???

NESTED DATA PARALLELISM

Blelloch's solution

Flatten all levels of nesting

concat   :: (ArithVector t) => t (t a) -> t a
unconcat :: (ArithVector t) => t (t a) -> t b -> t (t b)

bar' :: [[Float]] -> [[Float]]
bar' xss = unconcat xss (bar (concat xss))

This is manually impossible to define in a library

Need the compiler to understand nested structures

MEMORY LAYOUT ISSUES

Records are desugared to Product Types.

Very common to have array of tuples.

VecArray (Float, Float, Float) or VecList (Float, Float, Float)

Current hardware supports load and store vector instructions only for contiguous data

*Xeon Phi instruction set supports non contiguous loads and stores

Generally structure of arrays (SOA) layout is optimal over array of structures (AOS) layout

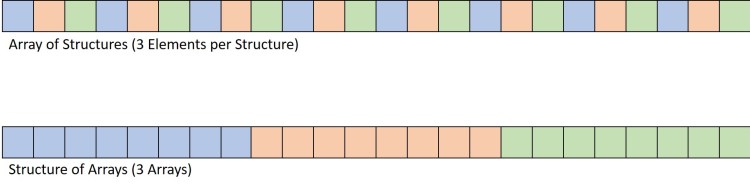
aosvsoa

This was not explored in the existing design of lift-vector

What are we looking for?

Tradeoff between :

An alternate programming model for programming vectors
A smart compiler (automatic vectorization)

Programming model

Data Layout
Syntax
Semantics

Data layout
- SOA over AOS
- Flatten nested parallelism
- Handle nested iterators (Palmer et al. 1995)
- ... more exploration

Semantics of the model
- Parallel by default
- Express divergent control flow (Karrenberg et al. 2017)
- Differentiate between convergent and divergent control flow
- Eagerly evaluated
- Leverage fusion wherever possible

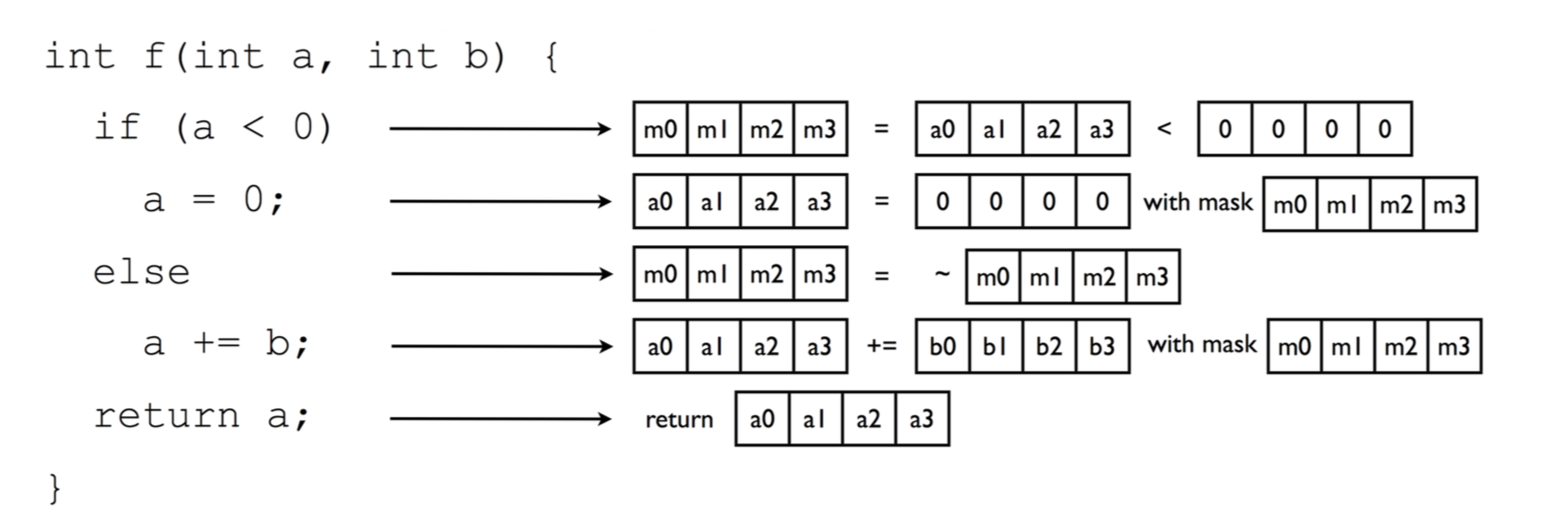
karrenberg

Whole function vectorization : control flow to data flow - Karrenberg, 2017

Syntax
- Declarative

Example

 -- all functions have parallel semantics unless specified otherwise
quicksort :: [Float] -> [Float]
quicksort [] = []
quicksort xs = 
  let pivot = srandom xs -- assume srandom pure & sequential
      small = select (p <= pivot) xs 
      large = select (p >  pivot) xs
   in (quicksort small) ++ [x] ++ (quicksort large)
         gang1                         gang2
 -- irregular data size but NDP can be made work efficient

Simply uses relational operators

Vector instruction CMPPSin SSE or VCMPPS in AVX

Merge sort is easier to parallelize

 [16 elems]    [16elems]
  8      8      8     8
 4 4    4 4    4 4   4 4 
mergesort_spmd xs
  let pivot    = smiddle xs 
      (x1, x2) = split xs
   in merge (mergesort_spmd x1) (mergesort_spmd x2)

merge :: [a] -> [a] -> [a] - Vectorized SIMD union

            xs = [9,7,8,1]
           /    |     \    \
          /     |      \    \
         /      |       \    \
        /       |        \    \
 (fork xs) (fork xs) (fork xs) (fork xs)

              foo = pack (9,7,8,1)
              bar = broadcast pivot
              (a,b)    foo < bar

An existing model on GPUs - SPMD (OpenCL)!

Intel ispc compiler - SPMD on SIMD

Why not just use ISPC?

No nested data parallelism
Impure, doesn't provide "safe" parallelism
A systems language replicating the entire C pointer model
Explicit uniform and varying memory annotations

So how do we implement our language?

Engineering decision

GHC might be coaxed to admit nested data parallelism (using source plugins) but SPMD requires major changes in the runtime.
Write a small functional frontend to LLVM which flattens the data as an optimizer pass.
Cajole the NESL runtime to an SPMD form and connect it to LLVM.

Conclusion

Haskell has shown[1] that performance at the cost of expressivity is not necessary

There is a always a sweet spot!

Reference

[1] Exploiting Vector Instructions with Generalized Stream Fusion. Mainland et al

THANK YOU FOR LISTENING

EXTRA SLIDES

DISADVANTAGES OF THE SPMD-NDP MODEL

complex control flow
V.IMP: Full vectorization can be disastrous
Flattening destroys the original loops and spoils a number of optimization opportunities

COST OF VECTORIZATION

Cost model
- Work and Depth (Blelloch, 1996)
- Compiler cost model (reducing pack, unpacks, scatters, gathers)

Throttled Superword Level Parallelism

Convert IR to SSA form

Cytron's algorithm

Hand made graph still SLP vectorized version slower than sequential version of the program

Throttle the vectorization by cutting the graph

Throttling is NP Hard

Can we auto vectorise faster?

Declarative Vector Programming

Abhiroop Sarkar

OUTLINE

Types of Parallel Machines

Single Instruction Multiple Data

WHY SIMD?

x86 Instruction Set

Compiler Support

Software Support

MASTER'S THESIS

Superword Level Parallelism in the Glasgow Haskell Compiler

Lift-Vector

Vectorised Containers

Vector Lists

Vector Arrays

ZIP

MAP

FOLD

SCAN

BLELLOCH SCAN

UPSWEEP

DOWNSWEEP

Lift Vector

DISADVANTAGES OF LIFT-VECTOR

EXAMPLE

NESTED DATA PARALLELISM

Blelloch's solution

MEMORY LAYOUT ISSUES

Example

Why not just use ISPC?

Engineering decision

Conclusion

Reference

DISADVANTAGES OF THE SPMD-NDP MODEL

COST OF VECTORIZATION

Throttled Superword Level Parallelism

Abhiroop Sarkar

@catamorphic

https://github.com/Abhiroop/lift-vector