G54FPP Mini Project

Abhiroop Sarkar

Calculating correct compilers

Program Calculation and correctness

Project spans two major areas

• Program Calculation
• Formal Verification

Program Calculation

Calculating the definitions of a function from their specifications

Lets take an example

What does an informal spec looks like?

An informal spec

Imagine a set P of people at a party. Say a subset C of P forms 
a celebrity clique if C is nonempty, everybody at the party 
knows every member of C, but members of C know only each other. 
Assuming there is such a clique at the party and given a binary 
predicate "knows" write a program for finding it.

Formalizing the previous spec

∅ ⊂ C ⊆ P and

(∀x ∈ P , y ∈ C :: x knows y ∧ (y knows x ⇒ x ∈ C ))

In Haskell

isClique ps cs  = and [p `knows` c | c <- cs, p <- ps] && 
                  and [not (c `knows` p) | c <- cs, p <- ps]

cclique ps = head (filter (isClique ps) (subseqs ps))

 -- Helper function
subseqs [ ] = [[ ]]
subseqs (x : xs) = map (x:) (subseqs xs) ++ subseqs xs

An example of calculation

 -- Base case will be empty
filter (isClique (p : ps)) (subseqs (p : ps)) 
= {definition of subseqs}
filter (isClique (p : ps)) (map (p:) (subseqs ps) ++ subseqs ps) 
= {since filter distributes over ++}
filter (isClique (p : ps)) (map (p:) (subseqs ps)) ++ 
filter (isClique (p : ps)) (subseqs ps)

Further simplification possible but we will be digressing from the main topic

So program calculation provides us with a form of equational reasoning tool

FORMAL VERIFICATION

The compcert C compiler

The Deepspec project

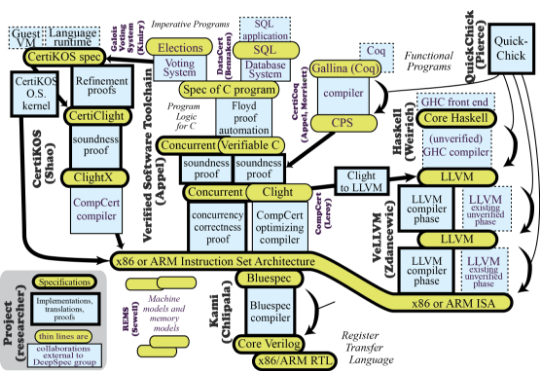
Compilers have some of the most in-depth specifications

Examples

• JLS - Java Language Specification
• Haskell 2010 Report/ Haskell 98
• Ecmascript specification

Question!

Can we then calculate a compiler from its specification??

Calculating correct compilers (Bahr and Hutton, 2016)

Hutton's Razor

data Expr = Val Int 
          | Add Expr Expr

 -- A very simple language

A simple evaluator for the language

eval :: Expr -> Int
eval (Val n) = n
eval (Add x y) = eval x + eval y

eval (Add (Val 1) + (Val 2))
= (eval (Val 1)) + (eval (Val 2))
= 1 + 2
= 3

Let's calculate a compiler for this language.

Step 1

We want a stack machine.

In Haskell, a list has stack like semantics: LIFO

So,

type Stack = [Int]

Specification:

Derive:
evalS :: Expr -> Stack -> Stack

such that
evalS x s = eval x : s                    (1)

Val n

 evalS (Val n) s
= { specification (1) }
 eval (Val n):s
= { definition of eval }
 n:s
= {define:pushS n s=n:s}
 pushS n s

Add x y

 evalS (Add x y) s
= { specification (1) }
 eval (Add x y):s
= { definition of eval }
(eval x + eval y):s

Induction Hypotheses for each element

 evalS x s' = eval x : s'

 evalS y s' = eval y : s'

Proceeding further,

 (eval x + eval y):s
= { define: addS (n:m:s) = (m+n):s }
 addS (eval y:eval x:s)
= { induction hypothesis for y }
 addS (evalS y (eval x : s))
= { induction hypothesis for x }
 addS (evalS y (evalS x s))

New stack based evaluator

evalS :: Expr -> Stack -> Stack
evalS (Val n) s = pushS n s
evalS (Add x y) s = addS (evalS y (evalS x s))


pushS :: Int -> Stack -> Stack
pushS n s = n:s


addS :: Stack -> Stack
addS (n:m:s) = (m+n):s


eval :: Expr -> Int
eval x = head (evalS x [])

STEP 2

Stack based machine to Continuation Passing Style

What is Continuation Passing Style (CPS)?

A normal function

function add(a, b) {
  return a + b;
}

The same function CPSed

function add_cps(a, b, done) {
  done(a + b);
}

Instead of

var result = add(1, 2);
// use result here

we now have,

add_cps(1, 2, function (result) {
  // use result here
});

And thats all about CPS.

Why CPS?

We have

type Cont = Stack -> Stack

And specification:

Derive
evalC :: Expr -> Cont -> Cont

such that
evalC x c s = c (evalS x s)      (2)

Calculating Val n

 evalC (Val n) c s
= { specification (2) }
 c (evalS (Val n) s)
= { definition of evalS }
 c (pushS n s)

Calculating (Add x y)

 evalC (Add x y) c s
= { specification (2) }
 c (evalS (Add x y) s)
= { definition of evalS }
 c (addS (evalS y (evalS x s)))
= { function composition }
 (c . addS) (evalS y (evalS x s))
= { induction hypothesis for y from (2) }
 evalC y (c . addS) (evalS x s)
= { induction hypothesis for x from (2)}
 evalC x (evalC y (c . addS)) s

The modified evaluator:

evalC :: Expr -> Cont -> Cont
evalC (Val n) c s = c (pushS n s)
evalC (Add x y) c s = evalC x (evalC y (c . addS)) s

evalS :: Expr -> Cont
evalS x = evalC x id

STEP 3

Defunctionalisation (Reynolds, 1972).

Go back two slides and extract the combinators

Substitute the combinators with direct style constructors

data Code where
  HALT :: Code
  PUSH :: Int -> Code -> Code
  ADD  :: Code -> Code

Substitute and rename the "eval" to "compile" to signify compilation

compile :: Expr -> Code
compile x = compile' x HALT

compile' :: Expr -> Code -> Code
compile' (Val n) c = PUSH n c
compile' (Add x y) c s = compile' x (compile' y (ADD c))

Compare and contrast!

evalS :: Expr -> Cont
evalS x = evalC x id

evalC :: Expr -> Cont -> Cont
evalC (Val n) c s = c (pushS n s)
evalC (Add x y) c s = evalC x (evalC y (c . addS)) s

defunctionalised to

compile :: Expr -> Code
compile x = compile' x HALT

compile' :: Expr -> Code -> Code
compile' (Val n) c = PUSH n c
compile' (Add x y) c s = compile' x (compile' y (ADD c))

Relationship between the two

exec :: Code -> Cont
exec HALT       = haltC
exec (PUSH n c) = pushC n (exec c)
exec (ADD c)    = addC (exec c)

exec (compile x) s    = evalS x s
exec (compile' x c) s = evalC x (exec c) s

Simplifying

exec (compile x) s    = eval x : s
exec (compile' x c) s = exec c (eval x:s)

We effectively calculated a compiler from its specification!

It uses the Calculus of Constructive Induction.

So it is correct by construction!

Beyond scope of the presentation

We can fuse the last two steps using a technique called Cutting Out Continuations (Hutton, 2016)

Formalized proofs in Coq: https://github.com/pa-ba/cps-defun

Research Questions

Can effects be specified?

Can we mechanize the calculation?

References

Calculating correct compilers (Bahr and Hutton, 2016)

Cutting out continuations (Hutton and Bahr, 2016)